Законы Ньютона. Правило сложения сил.

Рассмотрим движение материальной точки (рис. 46) в инерциальной системе отсчёта под действием сил, обусловленных взаимодействием точек с другими точками и телами (т. е. возникающих в результате взаимодействия материальных объектов).

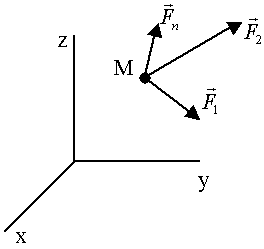
Рис.46.

Заметим, что при движении в неинерциальной системе отсчёта относительные движения частично определяются движением самой системы отсчёта.

Уравнения движения составляются на основе законов Ньютона.

Трактат «Математические начала натуральной философии»:

1687 г. – год возникновения теоретической механики.

Законы Ньютона – идеализированные законы природы, но для практики это допустимо в очень широких пределах.

Введём меры движения.

Количество движения – равно произведению массы m на вектор скорости точки:

,

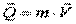где m = const > 0 – мера инертности материи.

Момент количества движения, относительно начала координат (рис. 47):

.

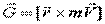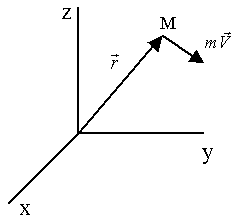
Рис.47.

Кинетическая энергия материальной точки:

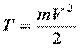(скаляр)

В дальнейшем покажем, что в ряде случаев движение точки наглядней описывается через 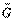или Т.

При формулировании законов Ньютона обозначаем:

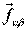- сила взаимодействия между точками 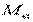и ;

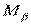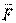- суммарная сила, приложенная к точке М , взаимодействующей со многими точками.

Первый закон Ньютона: материальная точка пребывает в состоянии покоя или равномерного прямолинейного движения относительно инерциальной системы отсчёта до тех пор, пока действующие на неё силы не изменят это состояние.

То есть изолированная точка либо покоится, либо движется прямолинейно и равномерно. Причина изменения движения – вне самой точки.

Второй закон Ньютона: производная по времени от количества движения материальной точки геометрически равна силе, приложенной к точке. Или, при постоянной массе, произведение массы точки на её абсолютное ускорение геометрически равно приложенной к материальной точке силе, т. е.

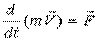или 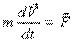, если m = const.

Связь кинематической величины – ускорения с динамической величиной – силой через коэффициент пропорциональности – массу.

Третий закон Ньютона: две любые материальные точки взаимодействуют друг с другом с силами, направленными по прямой, соединяющей эти точки, равными по величине и противоположно направленными (рис. 48).

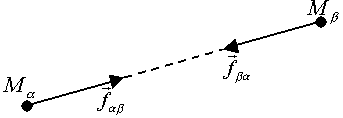
Рис.48.

Рассмотрим воздействие точки M1 c остальными точками (рис. 49).

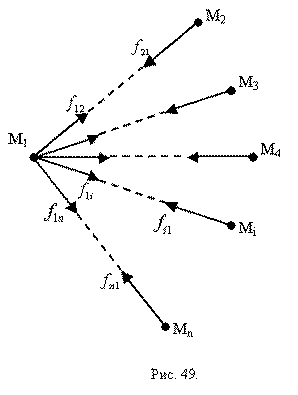
Для 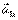имеем ускорение:

Принцип независимости действия сил:ускорение 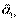, вызываемое силой 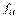, определяется только этой силой и не зависит от других сил.

Следствие:

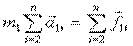; обозначая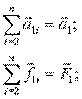

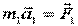
Геометрическая сумма ускорений 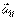, вызываемых силами взаимодействия точки М1 с остальными точками, пропорциональна геометрической сумме сил взаимодействия – правило параллелограмма для сложения сил.

От чего зависит сила ?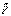

1) от координат точки в данный момент времени;

2) от предистории движения (старение);

3) от окружающей среды (температура);

4) сопротивление воздуха.

и т. д.

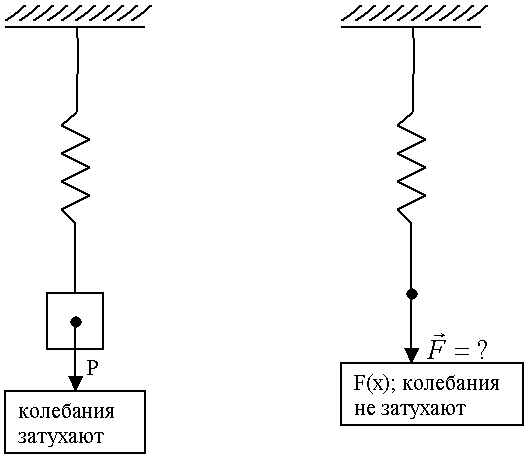
Рис.50.

Идеализация: силы зависят только от координат точки, от первых производных и явно от времени: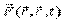

На практике – допустимо.

Развитие физики привело к изменению некоторых устаревших представлений и к выяснению границ области, в пределах которой справедлива механика Ньютона: его понятие об абсолютном пространстве заменено теперь понятием инерциальной системы отсчёта; установлено, что механика Ньютона – классическая механика – неприменима, если относительные скорости точек сравнимы со скоростью света [это область релятивистской или эйнштейновской механики]; неприменима механика классическая и к изучению явлений микромира [это область квантовой механики]. Но они основаны на классической механики. В остальных областях => классическая механика даёт достаточно точные результаты.

Контрольные вопросы:

1. Что называют динамикой?

2. Перечислите меры движения материальной точки

3. Сформулируйте законы Ньютона.

4. Каковы границы области применения классической механики Ньютона?