Дифференциальные уравнения движения точки

Рассмотрим движение свободной материальной точки в инерциальной системе отсчёта в декартовых координатах. Из 2-го закона Ньютона:

, ,

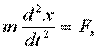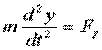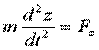
причём, Fx, Fy, Fz – могут зависеть от координат, первых производных, времени: .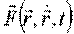

Если известен закон движения (например из кинематики):

, , ,

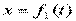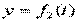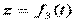то => Fx(t), Fy(t), Fz(t). Это первая (прямая) задача динамики точки.

Если известна сила, то для исследования движения необходимо интегрировать дифференциальные уравнения – это вторая (обратная) задача динамики точки.

Формы дифференциальных уравнений движения

1) 2-ой закон Ньютона – для количества движения.

2) Умножим на 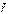(векторно):

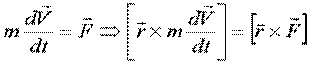
или 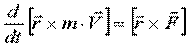- уравнение момента количества движения.

[Почему? – самостоятельно. Учесть ].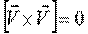

Производная по времени от момента количества движения геометрически равна моменту силы.

Подробная запись (координатная):

3) Умножим скалярно на элементарные перемещения :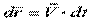

.

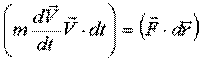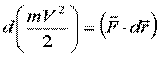- уравнение кинетической энергии.

Дифференциал кинетической энергии точки равен элементарной работе суммы сил, приложенных к точке, на действительном перемещении.

О первых интегралах (законы сохранения).

Из дифференциальных уравнений: функция координат, их производных по времени, являющаяся постоянной в силу уравнений (то есть её производная по времени равна нулю) => называется первым интегралом.

Получим такие условия.

Если 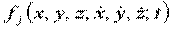- первый интеграл, то 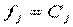и

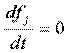
1) Если Fx = 0, то 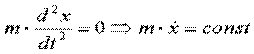, 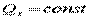- интеграл количества движения (закон сохранения количества движения).

2) Если 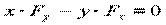(то есть проекция момента силы на ось z),

то из

,

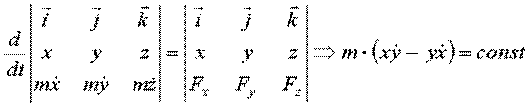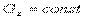- интеграл момента количества движения (закон сохранения момента количества движения).

3) Получим интеграл энергии.

.

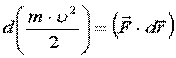Пусть правая часть есть полный дифференциал некоторой скалярной функции – потенциала силового поля .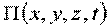

Тогда:

, , .

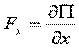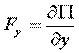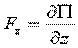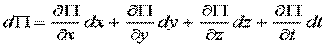
Работа:

.

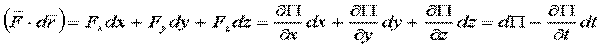Чтобы 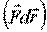было полным дифференциалом:

1) 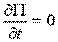- то есть поле стационарно (не зависит от t).

2) , 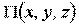с условиями из высшей математики:

; ;

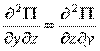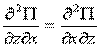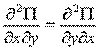
или

; ;

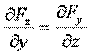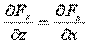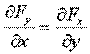
или

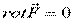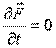Иначе: если и , то 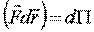и уравнение кинетической энергии будет в полных дифференциалах:

.

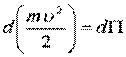Интегрируя:

.

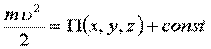Введём потенциальную энергию:

.

Тогда: 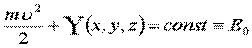- интеграл энергии (закон сохранения механической энергии).

Если силовое поле потенциально и стационарно, то сумма кинетической и потенциальной энергий свободной материальной точки равна постоянной.

Е0 – механическая энергия; находится из начальных условий.

Энергия сохраняется, то есть консервируется => поле называется консервативным.

Покажем, что работа сил консервативного поля не зависит от вида траектории, а равна разности значений функции П в конце и начале перемещения (рис.51).

Рис.51.

Работа:

,

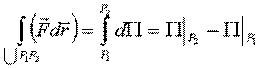что и требовалось доказать.

.

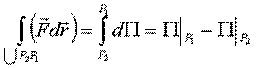Работа сил консервативного поля на замкнутом перемещении равна нулю (рис.52).

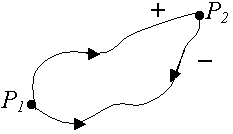
Рис.52.

Контрольные вопросы:

1. Сформулируйте прямую и обратную задачи динамики.

2. Напишите уравнение момента количества движения точки.

3. Что называется перовым интегралом дифференциального уравнения?

4. Какое силовое поле называется консервативным?