Производная по времени от кинетического момента системы свободных материальных точек равна сумме моментов всех внешних сил (главному моменту всех внешних сил).

Существенно: моменты количества движения и моменты сил вычисляются относительно общего неподвижного начала.

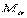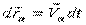3. Умножая скалярно уравнение движения точки на и суммируя:

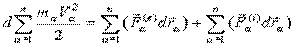
или

.

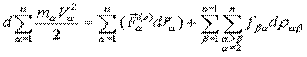Теорема об изменении кинетической энергии системы:

Дифференциал кинетической энергии системы свободных материальных точек равен сумме элементарных работ всех внешних и внутренних сил.

Интегралы уравнений движения системы:

1) Если равен нулю главный вектор внешних сил, то 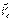= const, то есть центр масс системы свободных материальных точек движется равномерно и прямолинейно.

2) Если главный момент внешних сил равен нулю, то сохраняется кинетический момент системы свободных материальных точек:

.

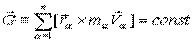3) Если внешние и внутренние силы консервативны, то

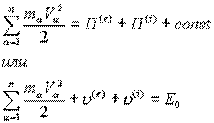
Здесь:

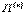- потенциал внешнего силового поля;

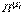- потенциал взаимодействия точек;

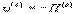- потенциальная энергия системы точек во внешнем поле;

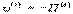- потенциальная энергия взаимодействующих точек.

Контрольные вопросы:

1. Чем математически являются общие теоремы динамики системы материальных точек?

2. Сформулируйте теорему об изменении кинетического момента системы.

3. Напишите интеграл энергии для системы материальных точек.