Общие теоремы динамики системы точек

Основные (общие) теоремы динамики систем свободных материальных точек являются уравнениями движения систем свободных материальных точек, т. е. математически дифференциальными уравнениями изменений основных мер движения.

1.Для точки 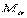уравнение движения относительно инерциальной системы отсчёта:

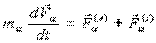
Перенесём все векторы, не изменяя их направления, в центр масс и сложим геометрически:

.

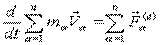Производная по времени от количества движения системы свободных материальных точек равна геометрической сумме внешних сил.Это теорема об изменении количества движения системы.

Так как 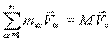то

.

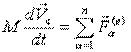Это уравнение движения центра масс системы материальных точек с массой, равной массе всей системы, к которой приложена сумма всех внешних сил (главный вектор внешних сил ) или теорема о движении центра масс.

2.Умножим уравнение движения точки 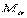слева векторно на 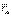и геометрически сложим, перенося векторы в центр масс:

.

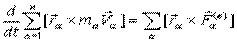Теорема об изменении кинетического момента системы: