ПОНЯТИЕ ПЕРВООБРАЗНОЙ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ.

Интегральное исчисление возникло из потребности создавать общий метод нахождения площадей, объемов и центров тяжестей. Основной задачей интегрального исчисления является нахождение функции по выражению ее дифференциала.

Одним из основных понятий интегрального исчисления является понятие первообразной.

Функция 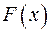называется первообразной функции 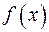, если в области определения функции 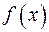имеет место тождество 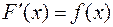. Таким образом, первообразная является решением задачи, обратной дифференцированию.

Пример. Найти первообразную функции .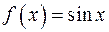

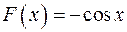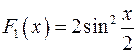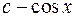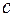Из таблицы производных находим . Легко убедиться, что решением задачи также является функция , и вообще любая функция вида , где – произвольная постоянная.

Приведенный пример показывает, что задача по отысканию первообразной имеет не единственное решение. Вопрос о различных видах первообразных решается теоремой.

Теорема. Разность двух первообразных функции 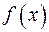есть величина постоянная.

Множество всех первообразных функции 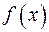называют неопределенным интегралом от функции 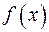и обозначают .

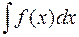Из доказанной теоремы следует, что если 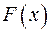– одна из первообразных функции 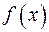, то

.

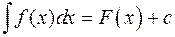Из определения, а также из правил дифференцирования следуют основные свойства неопределенного интеграла:

1. ;

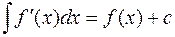2. ;

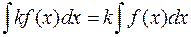3. .

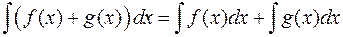ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ.

Из каждой формулы дифференцирования получается формула интегрирования. Например, из формулы 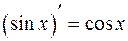вытекает

.

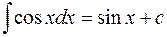Таким образом путем обращения таблицы производных приходим к таблице интегралов от основных элементарных функций:

1.

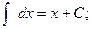
2.

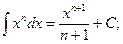
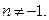
3.

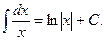
4.

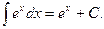
5.

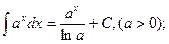
6.

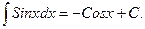
7.

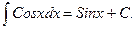
8.

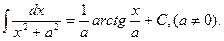
9.

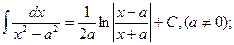
10.

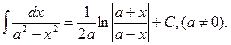
11.

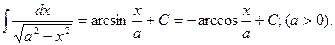
12.

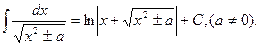
13.

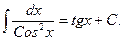
14.

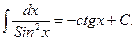
15.

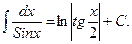
16.

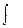
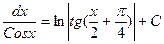
17.

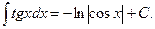
18.

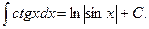
19.

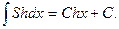
20.

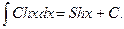
21.

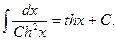
22.

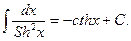
Приведенная таблица интегралов вместе со свойствами неопределенного интеграла позволяют в некоторых случаях производить операцию интегрирования.