Свойства определенного интеграла.
Из определения определенного интеграла вытекают следующие его свойства:
1. 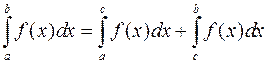 ;
;
2. 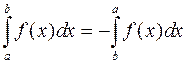 ;
;
3. 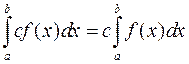 ;
;
4. 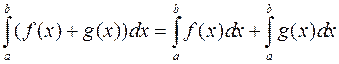 ;
;
5. Если 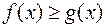 , то
, то 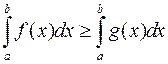 ;
;
6. 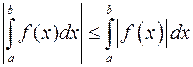 ;
;
7. Если 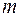 и
и 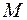 – наименьшее и наибольшее значения функции на интервале
– наименьшее и наибольшее значения функции на интервале 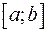 , то
, то
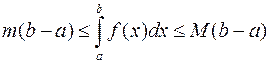 ;
;
МЕТОДЫ ИНТЕГРИРОВАНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Вычисление определенного интеграла сводится к нахождению неопределенного интеграла и дальнейшим вычислениям с пределами интегрирования.
Формула интегрирования по частям принимает вид
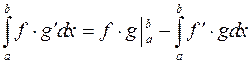 .
.
Пример. Вычислить 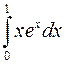 .
.
Положим 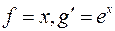 . Тогда
. Тогда 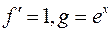 . По формуле получим
. По формуле получим
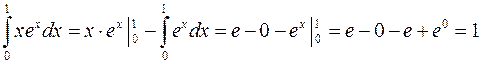 .
.
Формула замены переменной приобретает вид
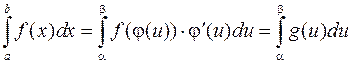 ;
;
где 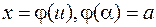 и
и 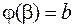 .
.
При применении формулы изменение пределов интегрирования делает ненужным возврат к старой переменной. Заметим, что функция 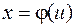 отображает интервал
отображает интервал 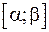 на интервал
на интервал 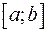 . Непременным условием является дифференцируемость функции
. Непременным условием является дифференцируемость функции 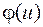 на интервале
на интервале 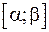 , а также ее монотонность на этом интервале.
, а также ее монотонность на этом интервале.
Пример. Вычислить 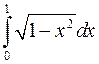 .
.
Воспользуемся тригонометрической подстановкой 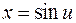 ,
, 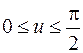 . Функция
. Функция 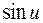 дифференцируема и монотонна внутри интервала
дифференцируема и монотонна внутри интервала 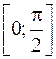 , причем
, причем 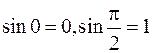 . Значит пределы интегрирования переменной
. Значит пределы интегрирования переменной 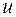 будут
будут 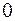 и
и 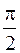 . Используя формулу (7), получим
. Используя формулу (7), получим
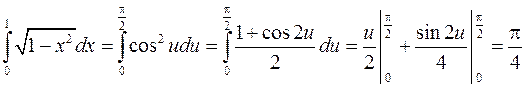 .
.
Дата добавления: 2017-03-12; просмотров: 1845;











