МЕТОД ИНТЕГРИРОВАНИЯ ПОДСТАНОВКОЙ.

1. Интегралы 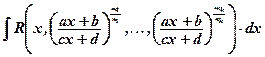, где R - рациональная функция; 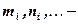целые числа, которые вычисляются с помощью подстановки 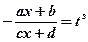; s - общий знаменатель дробей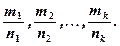

Пример. Найдите неопределённый интеграл .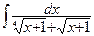

Выполняем подстановку: х + 1 = t⁴

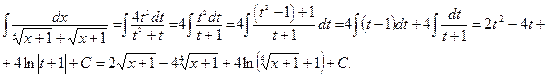
2. К интегралам от функций, рационально зависящих от тригонометрических функций, сводятся интегралы:

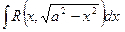подстановкой x=asint;

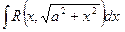- подстановкой x=atgx;

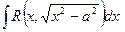- подстановкой x=a sec t.

3. Подстановка Эйлера 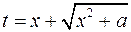преобразует интеграл .

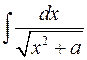к виду .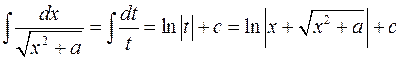

4. Интеграл 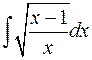приводится к интегралу от рациональной функции подстановкой 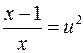, в результате которой получает вид

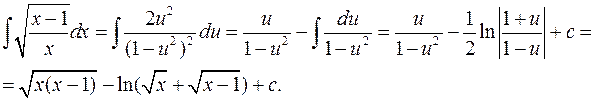
При вычислении интеграла от рациональной функции 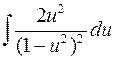использован метод интегрирования по частям при .

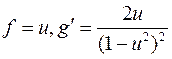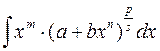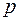5. Интеграл от биномиального дифференциала , где и 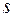– целые, а 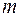и 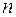– рациональные числа, приводится с помощью подстановки Чебышева к интегралу от рациональной функции в следующих случаях:

1) 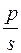– целое число (подстановка );

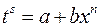2) 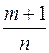– целое число (подстановка );

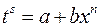3) 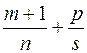– целое число (подстановка ).

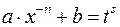В других случаях интеграл от биномиального дифференциала не выражается в конечном виде через элементарные функции.

Пример. Найдите неопределённый интеграл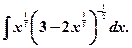

Здес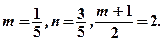ь Пусть 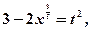откуда дифференцированием находим 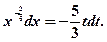Тогда

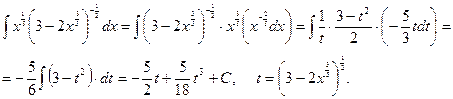
6. Подстановка 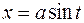или 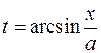преобразует интеграл 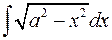к виду

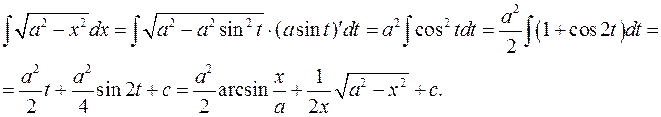
Определенный интеграл. Свойства