ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
1. Интегралы вида 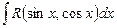 приводятся к интегралам от рациональных функций аргумента t универсальной тригонометрической подстановкой
приводятся к интегралам от рациональных функций аргумента t универсальной тригонометрической подстановкой 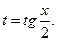 При этом используются соотношения:
При этом используются соотношения: 


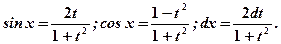
Пример. Найдите неопределённый интеграл 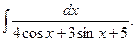
Полагаем 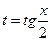 , тогда
, тогда
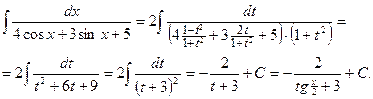
2. Если подынтегральное выражение представляет собой произведение двух тригонометрических функций с разными аргументами, то для вычисления интеграла используют формулы, позволяющие преобразовать произведение в сумму:
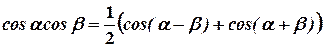
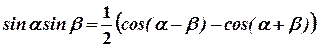
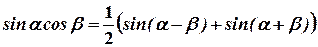
Пример.Найдите неопределённый интеграл 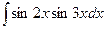 .
.
Решение. Применяем правило 2; разлагаем подынтегральную функцию на слагаемые, пользуясь тригонометрической формулой, затем интегрируем:
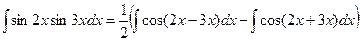
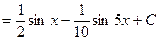
3а. Если подынтегральное выражение имеет вид: sinmxcosnx, причем одна из степеней нечетная, тогда нечетную степень преобразовывают к виду 2l+1, выделяя первую степень и делая соответствующую замену. Например: пусть нечетной является степень m, тогда имеем: m=2l+1. Sinmx=sin2l+1x=sin2lxsinx. Интеграл примет вид: 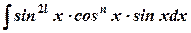 .
.
Таким образом получим: sinxdx=-dcosx и с учетом основного тригонометрического тождества наш интеграл преобразуется к виду: 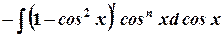 . Далее, возводя в степень и раскрывая скобки, мы получим интеграл от степенных функций, где переменной интегрирования будет cosx.
. Далее, возводя в степень и раскрывая скобки, мы получим интеграл от степенных функций, где переменной интегрирования будет cosx.
Пример.Найти неопределённый интеграл 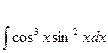
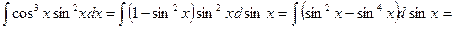
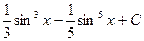
3б. Если же в подынтегральном выражении sinmxcosnx обе степеничётные, то для вычисления интеграла необходимо понизить степень один или несколько раз, воспользовавшись для этого формулами: 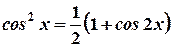 ;
; 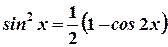 ;
; 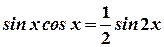
Пример. Найдите неопределённый интеграл 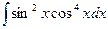
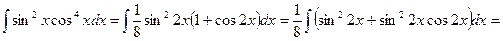
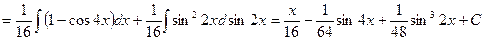
Дата добавления: 2017-03-12; просмотров: 1540;











