МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ В НЕОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ.
Этот метод получается из правила дифференцирования произведения 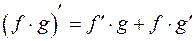 . Находя интеграл от производной произведения, получим
. Находя интеграл от производной произведения, получим
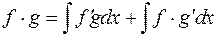 ,
,
откуда приходим к формуле интегрирования по частям
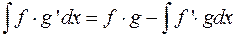 .
.
Значение формулы (2) состоит в том, что интеграл в правой части формулы может оказаться проще исходного.
Примеры.
Найти 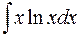 .
.
Допустим, что 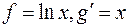 . Тогда
. Тогда 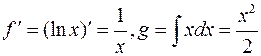 . После подстановки в формулу (2) получим
. После подстановки в формулу (2) получим
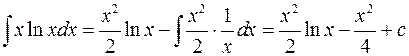 .
.
Найти 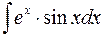 .
.
Пусть 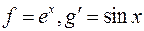 , тогда
, тогда 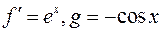 . По формуле (2) имеем
. По формуле (2) имеем
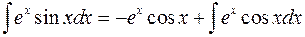 .
.
При повторном применении формулы интегрирования по частям получим
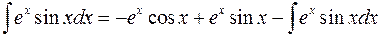 .
.
Разрешая данное уравнение относительно искомого интеграла, приходим к результату
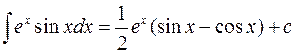 .
.
ИНТЕГРАЛЫ ОТ ФУНКЦИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЙ ТРЕХЧЛЕН.
1) 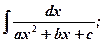 2)
2) 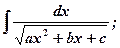 3)
3) 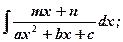 4)
4) 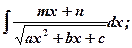
Интегралы 1), 2) сводятся к табличным путем выделения полного квадрата из квадратного трехчлена.
Интегралы 3), 4) сводятся к 1), 2) путем выделения из числителя производной квадратного трехчлена.
Пример. Найти неопределённый интеграл 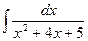
Выделив из квадрата трёхчлена полный квадрат x2+4x+5=x2+4x+4+1=(x+2)2+1, записав d(x+2) вместо dx, получим:
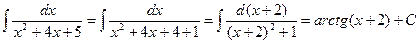
Пример.Найти неопределённый интеграл 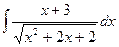 .
.
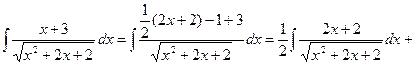
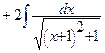 =
= 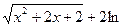
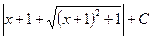 .
.
Дата добавления: 2017-03-12; просмотров: 1484;











