Глава 3. Отношения множеств
В главе 1 речь шла о том, что элементы множества могут находиться в некоторых отношениях между собой или с элементами других множеств. Были рассмотрены два таких отношения: принадлежность 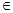 и включение
и включение 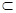 . Первое из них определяет связь между множеством и его элементами, а второе – между двумя множествами.
. Первое из них определяет связь между множеством и его элементами, а второе – между двумя множествами.
В самом общем смысле отношение означает какую-либо связь между предметами или понятиями. Отношения между парами объектов называют бинарными. Примерами бинарных отношений являются равенство (=), неравенства ( 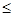 или <), а также такие выражения как «быть братом», «делиться на какое-то число», «входить в состав чего-либо» и т. п.
или <), а также такие выражения как «быть братом», «делиться на какое-то число», «входить в состав чего-либо» и т. п.
Для любого бинарного отношения можно записать соответствующее ему соотношение (для отношения неравенства соотношением будет 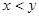 , для отношения «быть братом» соотношение запишется
, для отношения «быть братом» соотношение запишется 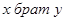 )
)
В общем виде бинарные отношения устанавливают соответствие элементов одного множества 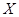 элементам другого множества
элементам другого множества 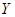 . Ясно, что такое отношение может быть задано некоторой совокупностью упорядоченных пар (
. Ясно, что такое отношение может быть задано некоторой совокупностью упорядоченных пар ( 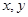 ), которые являются элементами множества
), которые являются элементами множества 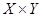 . Это вовсе не значит, что всегда нужно перечислять все такие пары. Часто отношение задается некоторым свойством, выраженным в словесной или символической форме.
. Это вовсе не значит, что всегда нужно перечислять все такие пары. Часто отношение задается некоторым свойством, выраженным в словесной или символической форме.
Если  – отношение, то соотношение
– отношение, то соотношение 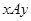 можно записать также в виде
можно записать также в виде 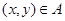 , где
, где 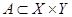 . Например, выражения
. Например, выражения 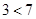 и
и 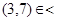 обозначают одно и тоже, но первое из них привычнее В то же время
обозначают одно и тоже, но первое из них привычнее В то же время 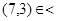 означало бы
означало бы 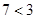 , что неверно. Таким образом, в общем случае переставлять элементы в паре (
, что неверно. Таким образом, в общем случае переставлять элементы в паре ( 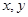 ) нельзя, что и подчеркивается названием этой пары – упорядоченной. Элемент
) нельзя, что и подчеркивается названием этой пары – упорядоченной. Элемент 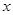 называют первой координатой, а элемент
называют первой координатой, а элемент 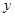 – второй координатой упорядоченной пары.
– второй координатой упорядоченной пары.
Множество первых координат 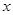 является областью определения (левой областью)
является областью определения (левой областью) 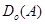 , а множество вторых координат
, а множество вторых координат 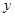 – областью значений (правой областью)
– областью значений (правой областью) 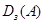 отношения
отношения  . Если
. Если 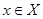 и
и 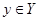 , то
, то 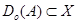 и
и 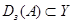 . В таких случаях говорят, что
. В таких случаях говорят, что  есть отношение от
есть отношение от 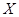 к
к 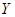 . Его называют также соответствием и обозначают
. Его называют также соответствием и обозначают 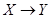 . Если
. Если 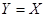 , то любое отношение
, то любое отношение 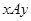 является подмножеством множества
является подмножеством множества 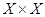 и называется отношением в
и называется отношением в 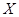 .
.
Пусть, например, 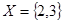 и
и 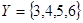 . Произведение этих множеств
. Произведение этих множеств 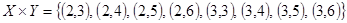 . Отношение = есть множество
. Отношение = есть множество 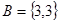 , а отношение > есть пустое множество
, а отношение > есть пустое множество 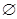 . Области определения и значений отношения
. Области определения и значений отношения  – это соответственно множества
– это соответственно множества 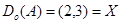 и
и 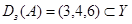 . Если область определения отношения совпадает с некоторым множеством
. Если область определения отношения совпадает с некоторым множеством 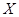 , то говорят, что отношение определено на
, то говорят, что отношение определено на 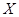 .
.
Очевидно, для отношения включения 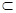 подмножеств универсума
подмножеств универсума 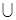 областью определения и областью значений служит множество подмножеств
областью определения и областью значений служит множество подмножеств 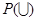 этого универсума.
этого универсума.
Заслуживают внимания три частных случая отношений в 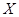 :
:
1) полное (универсальное) отношение 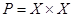 , которое имеет место для каждой пары (
, которое имеет место для каждой пары ( 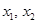 ) элементов из
) элементов из 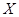 (например, отношение «работать в одном отделе» на множестве сотрудников данного отдела);
(например, отношение «работать в одном отделе» на множестве сотрудников данного отдела);
2) тождественное (диагональное) отношение 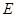 , равносильное
, равносильное 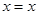 (например, равенство на множестве действительных чисел);
(например, равенство на множестве действительных чисел);
3) пустое отношение, которому не удовлетворяет ни одна пара элементов из 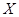 (например, отношение «быть братом» на множестве женщин).
(например, отношение «быть братом» на множестве женщин).
Очевидно, для любого отношения  в
в 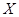 справедливо
справедливо 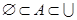 .
.
Рассмотрим отношение 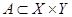 . Если
. Если 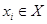 , то сечение по
, то сечение по 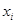 , отношения
, отношения  , обозначаемое
, обозначаемое 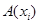 , есть множество
, есть множество 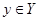 таких, что
таких, что 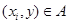 . Множество всех сечений отношения
. Множество всех сечений отношения  называют фактор-множеством множества
называют фактор-множеством множества 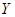 по отношению
по отношению  и обозначают
и обозначают 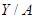 . Оно полностью определяет отношение
. Оно полностью определяет отношение  .
.
Пусть, например, 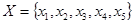 ;
; 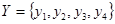 и
и
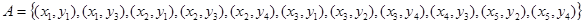 .Очевидно,
.Очевидно, 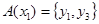 ;
; 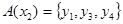 и т. д. Если записать под каждым элементом из
и т. д. Если записать под каждым элементом из 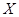 соответствующее сечение отношения
соответствующее сечение отношения  , то элементы второй строки образуют фактор-множество
, то элементы второй строки образуют фактор-множество 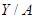 :
:
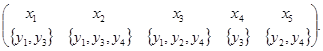
Объединение сечений по элементам некоторого подмножества 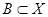 является сечением
является сечением 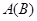 этого подмножества, т. е.
этого подмножества, т. е. 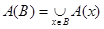 . Так для рассмотренного примера,
. Так для рассмотренного примера, 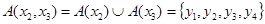
Так как отношение – это множества, то над ними можно выполнять все рассмотренные ранее теоретико-множественные операции. Кроме этого, определяются специфические для отношений операции: обращение и композиция.
Отношение, симметричное (обратное) некоторому отношению 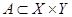 , обозначается через
, обозначается через 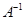 и представляет собой подмножество множества
и представляет собой подмножество множества 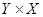 , образованное теми парами
, образованное теми парами 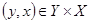 , для которых
, для которых 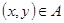 . Переход от
. Переход от  к
к 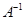 осуществляется взаимной перестановкой координат каждой упорядоченной пары. Так, обратное отношение для «
осуществляется взаимной перестановкой координат каждой упорядоченной пары. Так, обратное отношение для « 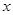 есть делитель
есть делитель 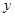 » будет «
» будет « 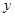 делится на
делится на 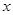 ». При переходе от
». При переходе от  к
к 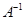 область определения становится областью значений, и наоборот.
область определения становится областью значений, и наоборот.
Пусть даны три множества 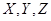 и два отношения
и два отношения 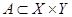 и
и 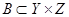 . Композиция отношений
. Композиция отношений  и
и  есть отношение
есть отношение 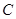 , состоящее из всех тех пар
, состоящее из всех тех пар 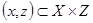 , для которых существует такое
, для которых существует такое 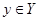 , что
, что 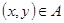 и
и 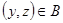 . Сечение отношения
. Сечение отношения 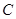 по
по 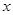 совпадает с сечением отношения
совпадает с сечением отношения  по подмножеству
по подмножеству 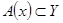 , т. е.
, т. е. 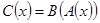 . Рассмотрим, например, два отношения:
. Рассмотрим, например, два отношения:
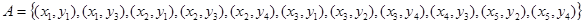 и
и
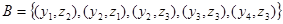 .
.
Очевидно,
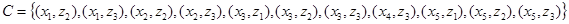 . Сечение
. Сечение 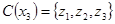 . С другой стороны,
. С другой стороны,
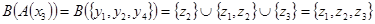 .
.
Композицию 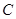 отношений
отношений  и
и  обычно записывают как
обычно записывают как 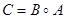 , тогда
, тогда 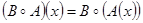 .
.
Композиция отношений обладает ассоциативным законом, т. е. 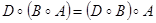 , но не коммутативна (
, но не коммутативна ( 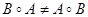 ). Можно также показать, что
). Можно также показать, что 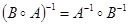 .
.
Пусть  – бинарное отношение в множестве
– бинарное отношение в множестве 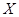 . Определим общие свойства таких отношений, которые должны выполняться для всех
. Определим общие свойства таких отношений, которые должны выполняться для всех 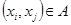 . Говорят, что
. Говорят, что 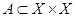 :
:
1) рефлексивно, если 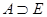 (
( 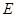 – тождественное отношение), т. е. оно всегда выполняется между объектом и им самим:
– тождественное отношение), т. е. оно всегда выполняется между объектом и им самим: 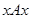 (равенство, самообслуживание);
(равенство, самообслуживание);
2) антирефлексивно, если 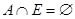 , т. е. может выполняться только для несовпадающих объектов: из
, т. е. может выполняться только для несовпадающих объектов: из 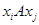 следует
следует 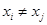 (строгое неравенство);
(строгое неравенство);
3) симметрично, если 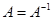 , т. е. при выполнении соотношения
, т. е. при выполнении соотношения 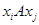 выполняется и соотношение
выполняется и соотношение 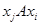 (расстояние между двумя точками);
(расстояние между двумя точками);
4) асимметрично, если 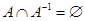 , т. е. из двух соотношений
, т. е. из двух соотношений 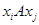 и
и 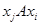 по меньшей мере одно не выполняется (строгое включение); если отношение асимметрично, то оно и антирефлексивно;
по меньшей мере одно не выполняется (строгое включение); если отношение асимметрично, то оно и антирефлексивно;
5) антисимметрично, если 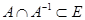 , т. е. оба соотношения
, т. е. оба соотношения 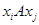 и
и 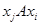 выполняются одновременно только тогда, когда
выполняются одновременно только тогда, когда 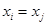 (нестрогое неравенство);
(нестрогое неравенство);
6) транзитивно, если 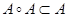 , т. е. из
, т. е. из 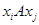 и
и 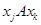 следует
следует 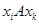 («быть родственником»).
(«быть родственником»).
Кроме рассмотренных ранее отношений принадлежности и включения рассмотрим отношения эквивалентности, порядка и толерантности.
Отношение эквивалентности представляет собой замену таких обыденных слов как «одинаковость», «неразличимость», «взаимозаменяемость». Эквивалентность обозначается знаком ~. При этом 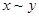 означает, что упорядоченная пара
означает, что упорядоченная пара 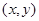 принадлежит множеству
принадлежит множеству 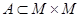 , являющимся отношением эквивалентности в множестве
, являющимся отношением эквивалентности в множестве 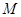 . Эквивалентность удовлетворяет условиям рефлексивности, симметричности, транзитивности, что записываются следующим образом:
1)
. Эквивалентность удовлетворяет условиям рефлексивности, симметричности, транзитивности, что записываются следующим образом:
1) 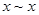 (рефлексивность); 2) если
(рефлексивность); 2) если 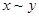 , то
, то 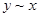 (симметричность); 3) из
(симметричность); 3) из 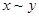 и
и 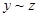 следует
следует 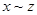 (транзитивность).
(транзитивность).
Важнейшее значение эквивалентности состоит в том, что это отношение определяет признак, который допускает разбиение множества 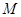 на непересекающиеся подмножества, называемые классами эквивалентности. Наоборот, всякое разбиение множества
на непересекающиеся подмножества, называемые классами эквивалентности. Наоборот, всякое разбиение множества 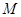 на непересекающиеся подмножества определяет между элементами этого множества некоторое отношение эквивалентности.
на непересекающиеся подмножества определяет между элементами этого множества некоторое отношение эквивалентности.
Например, отношение «проживать в одном доме» в множестве жителей города является эквивалентностью и разбивает это множество на непересекающиеся подмножества людей, являющихся соседями по дому. Примерами отношений эквивалентности могут служить подобие или равенство треугольников на плоскости, параллельность прямых, утверждение «быть таким же» и т. п.
Все элементы, принадлежащие некоторому классу 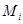 разбиения
разбиения 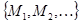 множества
множества 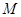 , связаны отношением эквивалентности. Они взаимозаменяемые в том смысле, что любой из этих элементов определяет данный класс, т. е. может служить его представителем (эталоном). Подмножество из
, связаны отношением эквивалентности. Они взаимозаменяемые в том смысле, что любой из этих элементов определяет данный класс, т. е. может служить его представителем (эталоном). Подмножество из 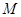 , содержащее по одному и только по одному элементу из каждого класса некоторого разбиения, называют системой представителей соответствующего отношения эквивалентности. Множество всех классов разбиения множества
, содержащее по одному и только по одному элементу из каждого класса некоторого разбиения, называют системой представителей соответствующего отношения эквивалентности. Множество всех классов разбиения множества  , определяемого отношением эквивалентности
, определяемого отношением эквивалентности 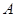 , образует фактор-множество
, образует фактор-множество 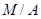 . Например, отношение параллельности определяет разбиение множества прямых на плоскости на классы, каждый из которых образован множеством параллельных между собой прямых и характеризуется некоторым направлением (следует также считать, что прямая параллельна самой себе). Любая из параллельных прямых может служить представителем данного класса, а само направление есть класс эквивалентности. Множество всех направлений составляет фактор-множество множества всех прямых по отношению параллельности.
. Например, отношение параллельности определяет разбиение множества прямых на плоскости на классы, каждый из которых образован множеством параллельных между собой прямых и характеризуется некоторым направлением (следует также считать, что прямая параллельна самой себе). Любая из параллельных прямых может служить представителем данного класса, а само направление есть класс эквивалентности. Множество всех направлений составляет фактор-множество множества всех прямых по отношению параллельности.
Произвольное отношение эквивалентности определяет на некотором множестве обобщенную форму равенства. Классы эквивалентности состоят из всех тех элементов, которые неразличимы с точки зрения данного отношения эквивалентности. Разбиение множества на классы означает идентификацию эквивалентных между собой элементов. При этом каждый класс определяется его представителем (эталоном) и отождествляется с некоторым общим свойством или совокупностью свойств (параметров) входящих в него элементов (направление по отношению параллельности и т. п.).
Предельным случаем отношения эквивалентности является тождественное равенство. Единственный элемент, равный какому-либо данному элементу, есть этот самый элемент. Следовательно, имеем самое полное разбиение, при котором классы эквивалентности содержат только по одному элементу исходного множества.
Отношение порядка принято обозначать символом 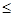 . Запись
. Запись 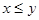 означает, что пара (
означает, что пара ( 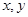 ) принадлежит множеству
) принадлежит множеству 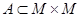 , являющемуся отношением порядка в множестве
, являющемуся отношением порядка в множестве  , причем
, причем 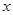 предшествует
предшествует 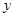 (или
(или 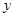 следует за
следует за 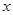 ). Отношение порядка обладает свойствами рефлексивности, транзитивности и антисимметричности, которые в принятых обозначениях записываются следующим образом: 1)
). Отношение порядка обладает свойствами рефлексивности, транзитивности и антисимметричности, которые в принятых обозначениях записываются следующим образом: 1) 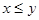 (рефлексивность); 2) если
(рефлексивность); 2) если 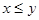 и
и 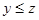 то
то 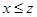 (транзитивность); 3) из
(транзитивность); 3) из 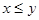 и
и 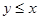 следует
следует 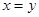 (антисимметричность).
(антисимметричность).
Множество, на котором определено отношение порядка, называют упорядоченным, и говорят, что порядок введен этим отношением. Множество совершенно упорядочено, если для любых двух его элементов имеет место, по крайней мере, 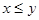 или
или 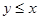 (его называют также цепью). Например, множество натуральных или действительных чисел с естественным отношением порядка
(его называют также цепью). Например, множество натуральных или действительных чисел с естественным отношением порядка 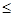 , множество значений длин волн на шкале радиоприемника и т п.
, множество значений длин волн на шкале радиоприемника и т п.
В общем случае может оказаться, что для некоторых пар ( 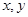 ) ни одно из соотношений
) ни одно из соотношений 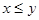 и
и 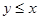 не имеет места (такие элементы называют несравнимыми). Тогда говорят, что множество частично упорядочено. Типичным примером частичного порядка является отношение «быть делителем», поскольку не все пары элементов из множества целых чисел находятся в отношении «быть делителем».
не имеет места (такие элементы называют несравнимыми). Тогда говорят, что множество частично упорядочено. Типичным примером частичного порядка является отношение «быть делителем», поскольку не все пары элементов из множества целых чисел находятся в отношении «быть делителем».
Отношение, наделенное свойствами транзитивности и антирефлексивности (следствиями этих двух свойств являются также асимметричность и антисимметричность), называют отношением строгого порядка и обозначают символом <. Свойство антирефлексивности означает, что элемент множества не может сравниваться сам с собой (как в случае строгого неравенства или строгого включения). В отличие от него отношение 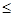 называют нестрогим порядком. Между отношениями строгого и нестрогого порядка имеют место соотношения (
называют нестрогим порядком. Между отношениями строгого и нестрогого порядка имеют место соотношения ( 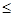 )=
)= 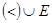 и
и 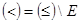 , где
, где 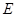 – тождественное отношение.
– тождественное отношение.
Отношение строгого порядка характерно для различного рода иерархий с подчинением одного объекта другому (или другим). Если для некоторой совокупности элементов из  справедливо соотношение
справедливо соотношение 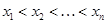 , то в соответствии со свойством транзитивности
, то в соответствии со свойством транзитивности 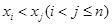 , т. е. отношение строгого порядка обусловливает как прямое, так и косвенное подчинение по старшинству.
, т. е. отношение строгого порядка обусловливает как прямое, так и косвенное подчинение по старшинству.
Элементы любого конечного множества  можно пронумеровать порядковыми числами
можно пронумеровать порядковыми числами 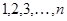 . Для счетного множества нумерацию следует понимать как взаимнооднозначное отображение множества натуральных чисел
. Для счетного множества нумерацию следует понимать как взаимнооднозначное отображение множества натуральных чисел 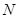 на М, которое каждому числу
на М, которое каждому числу 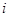 ставит в соответствие некоторый элемент
ставит в соответствие некоторый элемент 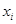 из
из  . Упорядоченное таким отображением множество
. Упорядоченное таким отображением множество 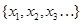 называется последовательностью (конечной или бесконечной). Элемент
называется последовательностью (конечной или бесконечной). Элемент 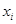 из
из  называют членом последовательности с индексом
называют членом последовательности с индексом 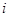 .
.
Нумерация элементов множества устанавливает совершенно строгий порядок на этом множестве. Например, на спортивных соревнованиях жеребьевкой каждому спортсмену ставится в соответствие номер; термины в предметном указателе располагаются в соответствии с порядком следования букв алфавита (здесь предполагается соответствие между последовательностью букв и отрезком натурального ряда чисел).
Отношение толерантности на множестве  , обозначаемое символом
, обозначаемое символом 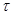 , удовлетворяет свойствам рефлексивности и симметричности. Упорядоченная пара
, удовлетворяет свойствам рефлексивности и симметричности. Упорядоченная пара 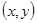 принадлежит множеству
принадлежит множеству 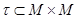 , если: 1)
, если: 1) 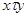 и 2) из
и 2) из 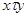 следует
следует 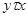 . Для этого отношения, в отличие от эквивалентности, транзитивность не обязательна, и значит эквивалентность есть частный случай толерантности.
. Для этого отношения, в отличие от эквивалентности, транзитивность не обязательна, и значит эквивалентность есть частный случай толерантности.
Отношение толерантности представляет собой перевод интуитивных представлений о сходстве и неразличимости в ранг математических понятий. Каждый объект неразличим сам с собой (рефлексивность), а сходство двух объектов не зависит от того, в каком порядке они сравниваются (симметричность). В то же время, если один объект сходен с другим, а другой сходен с третьим, то это вовсе не означает, что все они обязательно сходны между собой, т. е. свойство транзитивности может не выполняться.
Развлекательным примером толерантности является популярная задача «превращение мухи в слона» (муха–мура–тура–тара–кара–каре–кафе–кафр–каюр–каюк–крюк–крок–срок–сток–стон–слон). Здесь отношение толерантности определяется сходством между четырехбуквенными словами, если они отличаются только одной буквой. Если определить отношение между словами как наличие хотя бы одной общей буквы, то толерантными будут пересекающиеся слова кроссворда.
Сходство между различными объектами имеет точный смысл только тогда, когда указана совокупность признаков, относительно которой это сходство устанавливается. Два объекта считаются сходными (толерантными), если они обладают хотя бы одним общим признаком.
Пусть 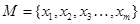 множество объектов и
множество объектов и 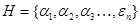 множество признаков. Каждому элементу
множество признаков. Каждому элементу 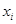 из
из  соответствует некоторое подмножество
соответствует некоторое подмножество 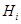 признаков (
признаков ( 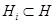 ). Следовательно, сходство между объектами
). Следовательно, сходство между объектами 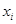 и
и 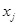 определяется толерантностью соответствующих им подмножеств
определяется толерантностью соответствующих им подмножеств 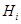 и
и 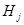 из
из 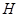 , т. е. условием
, т. е. условием 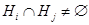 .
.
Если рассматривать соответствие между объектами и признаками как бинарное отношение 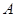 между множеством объектов
между множеством объектов  и множеством признаков
и множеством признаков 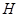 , то элементами
, то элементами 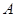 будут упорядоченные пары
будут упорядоченные пары 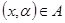 , в каждой из которых первая координата является объектом, а вторая – признаком. Очевидно, множество
, в каждой из которых первая координата является объектом, а вторая – признаком. Очевидно, множество 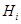 признаков объекта
признаков объекта 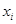 является сечением
является сечением 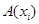 этого отношения, т. е.
этого отношения, т. е. 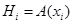 . Все такие сечения полностью определяют бинарное отношение
. Все такие сечения полностью определяют бинарное отношение 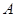 .
.
Итак, толерантность 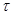 на множестве объектов
на множестве объектов  можно задать с помощью некоторого всюду определенного бинарного отношения
можно задать с помощью некоторого всюду определенного бинарного отношения 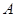 от
от  к
к 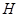 следующим образом: для любой пары объектов
следующим образом: для любой пары объектов 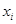 и
и 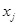 из
из  имеет место
имеет место 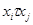 , если и только если
, если и только если 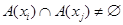 .
.
Дата добавления: 2016-09-06; просмотров: 6940;











