Пересечение множеств

Пересечение множеств А и В обо­значают А В. Таким образом, по оп­ределению, А В = {х|х А и х В).

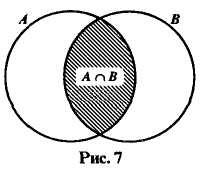
Если изобразить множества А и В при помощи кругов Эйлера, то пере­сечением данных множеств является заштрихованная область (рис. 7).

В том случае, когда множества А и В не имеют общих эле­ментов, говорят, что их пересечение пусто и пишут: А В = Ø.

Выясним, как находить пересечение множеств в конкрет­ных случаях.

Если элементы множеств А и В перечислены, то, чтобы найти А В, достаточно перечислить элементы, которые од­новременно принадлежат множеству А и множеству В, т.е. их общие элементы.

А как быть, если множества заданы характеристическими свойствами своих элементов?

Из определения пересечения следует, что характеристиче­ское свойство множества А В составляется из характеристи­ческих свойств пересекаемых множеств с помощью союза «и».

Найдем, например, пересечение множества А - четных натуральных чисел и множества В - двузначных чисел. Ха­рактеристическое свойство элементов множества А - «быть четным натуральным числом», а характеристическое свой­ство элементов множества В - «быть двузначным числом». Тогда, согласно определению, элементы пересечения данных множеств должны обладать свойством «быть четными нату­ральными и двузначными числами». Таким образом, множе­ство А В состоит из четных двузначных чисел (союз «и» в данном случае можно опустить). Полученное множество не пусто. Например, 24 А В, поскольку число 24 четное и двузначное.

Рассмотрим теперь случай, когда находят пересечение множества А и его подмножества В. Легко видеть, что тогда А В - В и, следовательно, характеристическое свойство элементов множества А В будет таким, как и свойство эле­ментов множества В.