Устойчивость сжатых стержней

7.1 Устойчивость равновесия сжатого стержня

В нагруженных телах при любом деформированном состоянии имеет место равновесие между внешними и внутренними силами. Де­формированное состояние характеризуется формой тела, формой равновесия. Под устойчивостью понимают свойство тела сохранять свою первоначальную форму равновесия.

Рассмотрим формы равновесия при сжатии стержней. При сжа­тии короткого жесткого стержня (рис. 7.1, а) его рассчитывают на прочность и жесткость по формулам для осевого сжатия. При сжатии стержня, имеющего достаточно большую длину по срав­нению с поперечными размерами, возможно следующее. Пока сжи­мающая сила мала и ось стержня (рис. 7.1, б, г) строго прямолиней­на, стержень находится в состоянии устойчивого равновесия. При сжимающей силе, равной некоторому критическому значению 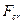ось стержня искривляется (рис. 7.1, в, д). В этом случае начальная (расчетная) прямолинейная форма равновесия становится неустой­чивой. Критической силой 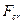называется наименьшее значение сжимаю­щей силы, при котором ось сжатого стержня теряет прямолинейность. По определению Л. Эйлера, критическая сила — это сжимающая сила, требуемая для самого малого наклонения колонны.

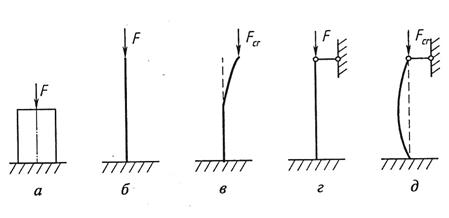
Рис. 7.1

Понятие устойчивости не следует смешивать с понятием прочно­сти; каждое из них имеет самостоятельное значение. Например, сжа­тый стержень при действии силы, большей критической, изогнется, но деформации его будут упругими, и после снятия нагрузки он вос­становит свою первоначальную форму. Потеря устойчивости в этом случае не связана с потерей прочности. В иных случаях потеря устой­чивости, изменение формы элемента может привести к разрушению или невозможности выполнения элементом своих функций.

При расчете на устойчивость сжатых стержней прежде всего нуж­но уметь определять критическую силу 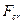. Ее рассматривают как пре­дельную нагрузку. Допускаемая нагрузка должна быть, естественно, меньше критической:

,

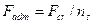где 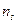— коэффициент запаса устойчивости, значение которого при­нимают большим значения коэффициента запаса прочности 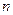, так как учитывают дополнительные неблагоприятные факторы: началь­ную непрямолинейность оси стержня, возможный эксцентриситет действия сжимающей нагрузки и др. Для стальных стержней прини­мают 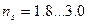; для хрупких материалов — до .

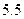Потеря устойчивости является причиной многих аварий и ката­строф; она возможна при кручении, изгибе и сложных деформациях.

7.2 Определение критической силы. Задача Эйлера

Задача по определению критической силы Fcr впервые была ре­шена Л. Эйлером в 1744 г. Рассмотрим сжатый стержень при условии, что он изогнулся (рис. 7.2, а), т.е. сжимающая сила равна критиче­ской. Для изучения изгиба используем дифференциальное уравнение изогнутой оси стержня:

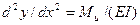
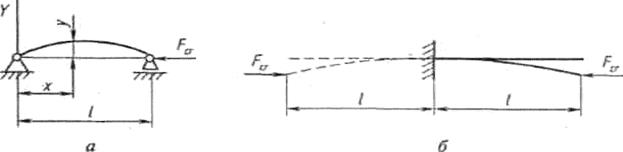
Рис. 7.2

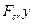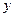Изгиб происходит в плоскости минимальной жесткости, т.е. по­перечные сечения будут поворачиваться вокруг той оси, относитель­но которой момент инерции I имеет минимальное значение. Изги­бающий момент МИ по абсолютной величине в любом сечении равен , где — прогиб поперечного сечения. Так как прогиб 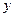и вторая производная от него 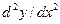при любом направлении оси OY всегда имеют противоположные знаки, уравнение выразим в следую­щем виде:

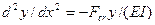
Введя обозначение

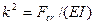
представим уравнение в виде 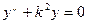. Это линейное диффе­ренциальное уравнение второго порядка. Его общее решение имеет вид

.

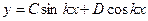Для определения постоянных интегрирования 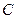и 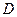используем известные граничные условия, а именно, условия крепления на кон­цах стержня: пр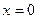и и 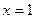прогиб отсутствует, т.е. .

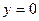Подставив в уравнение 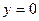(при 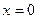), определим, что 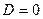, а стержень изгибается по синусоиде 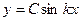. При втором гра­ничном услови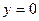и ( при 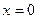) найдем: 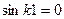. Полученное соот­ношение справедливо, ес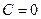ли или 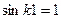. Если считать 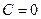, то при 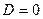прогиб во всех поперечных сечениях по длине стержня при любых значениях 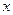отсутствует, что противоречит исходной пред­посылке. Выражение 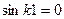справедливо, когда ,

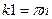где 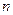— про­извольное целое число ( 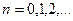). Подставив значение 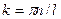, получим:

.

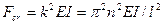Чтобы стержень сохранял криволинейную форму, необходимо, чтобы сила была отлична от нуля, т.е. 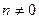. С практической точки зре­ния интерес представляет наименьшее значение критической силы, при действии которой происходит искривление оси стержня, потеря устойчивости. При 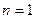получаем наименьшее значение критической силы:

.

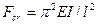Используя особенности упругой линии, можно распространить полученное решение на другие случаи закрепления стержня. Так, если стержень на одном конце жестко защемлен, а на другом — свобо­ден (рис. 7.2, б), то упругую линию стержня легко привести путем зеркального отображения относительно заделки к упругой линии шарнирно закрепленного стержня (рис. 7.2, а). Очевидно, что критиче­ская сила стержня с таким закреплением длиной l будет равна крити­ческой силе шарнирно закрепленного стержня длиной .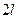

Общее выражение критической силы для сжатого стержня в обоб­щенном виде с учетом его типа крепления примет вид:

,

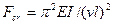где 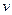— коэффициент приведения длины стержня (коэффициент Ясин­ского), т.е. число, показывающее, во сколько раз нужно изменить дли­ну шарнирно опертого с обоих концов стержня (рис. 7.3, б), чтобы критическая сила его была равна критической силе стержня с кон­кретными условиями закрепления. Чаще всего концы сжимаемых стержней закрепляют одним из четырех способов, показанных на рис. 7.3. Коэффициенты приведения длины указаны на схемах креп­ления. Наиболее чувствительным к потере устойчивости является кре­пление, представленное на рис. 7.3, а, наименее чувствительным — крепление, показанное на рис. 7.3, г.

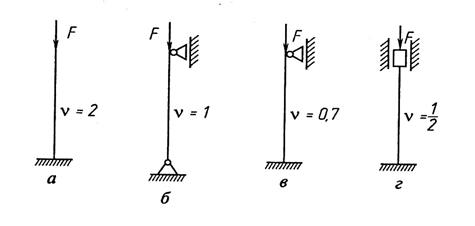
Рис. 7.3