Абсолютная устойчивость нелинейных систем в случае, когда W(p) не является рациональной функцией.

Если математическая модель линейного блока содержит уравнения с запаздывающим аргументом, то передаточная функция W(p) будет включать трансцендентные или иррациональные звенья или и те и другие. В этом случае динамика линейного блока системы может быть описана интегральным уравнением:

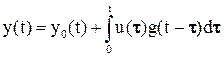
Где 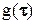- весовая функция линейного блока L (обратное преобразование Лапласа от W(p)).

Функция у₀(t) зависит от начальных данных и описывает собственные колебания линейного блока.

Ограничения на свойства линейного блока имеют вид:

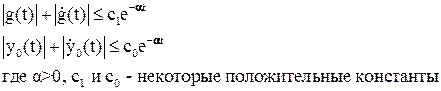
Удобнее ограничения сформулировать в следующей форме. Пусть ε – малое положительное число. Все особые точки передаточной функции W(p) находятся в левой полуплоскости на расстоянии больше ε от мнимой оси. Подчеркнем, что в данной задаче кроме полюсов функция W(p) может иметь существенно особые точки и точки ветвления.

Пусть функция N(x) находится в секторе S(μ₀):

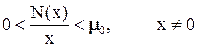
N(x) – кусочно-непрерывная функция.

Теорема.

При выполнении указанных ограничений для абсолютной устойчивости положения равновесия достаточно, чтобы для некоторого действительного числа θ выполнялось неравенство В.М.Попова:

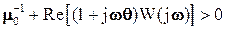
Существенное ограничение на передаточную функцию состоит в том, что W(p) не может иметь полюсов на мнимой оси. Однако, во многих важных случаях его можно преодолеть. Предположим, что W(p) имеет полюса на мнимой оси. Практический интерес представляют случаи, когда W(p) включает: интегрирующее звено, два интегрирующих звена, консервативное звено, консервативное и интегрирующее звенья. Предположим, что для некоторого положительного числа λ передаточная функция:

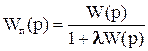
Удовлетворяет вышеуказанным ограничениям. То есть в W_п(p) под влиянием величины λ расположенные на мнимой оси полюса W(p) сдвинулись с мнимой оси в левую полуплоскость. Подчеркнем, что существенно особые точки и точки ветвления не изменят своего положения.

Если нелинейная функция N(x) находится в секторе 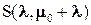, то посредством эквивалентного преобразования можно перейти к задаче в секторе S(μ₀), где линейный блок имеет передаточную функцию W_п(p).

Обзор основных результатов.

Ключевую роль в решении задачи абсолютной устойчивости имеют два основных неравенства. Неравенство В.М.Попова и неравенство В.А.Якубовича.

Выполнение неравенства В.А.Якубовича является достаточным условием устойчивости для очень широкого класса нелинейностей в базовом секторе. В частности нелинейность N(x) может быть гистерезисная и может быть нестационарная. Кроме того она может иметь разрывы первого рода.

Доказывается, что при выполнении неравенства В.А.Якубовича система имеет большие возможности при отработке внешнего воздействия.

В частности, если система подвержена периодическому или почти периодическому внешнему воздействию, то у системы существует периодический или почти периодический или просто ограниченный предельный режим (т.е. при t→∞).

Выполнение неравенства В.М.Попова гарантирует достаточные условия для более узкого класса элементов, которые были описаны выше. В частности, если нелинейность гистерезисная, то необходимо потребовать монотонные изменения функции и обход петли гистерезиса в определенном направлении.

Что касается внешнего воздействия, то в случае почти периодического внешнего воздействия система может не иметь единственного предельного режима, хотя изменение выходной координаты всегда остается ограниченным.

Заключение.

В параграфе мы рассматривали только достаточное условие абсолютной устойчивости. Разумеется, для теории управления было бы исключительно важно располагать необходимыми и достаточными условиями абсолютной устойчивости столь же простыми и наглядными, как критерий В.М.Попова. Таким образом, было бы получено полное обобщение критерия Найквиста для нелинейных систем. Однако, задача получения необходимых и достаточных условий оказалась исключительно трудна. И в настоящее время, несмотря на то, что прошло уже почти пол века с момента появления основополагающей работы В.М.Попова и в этой области работало большое число математиков, главным образом в СССР и США, такие условия получены только в некоторых частных случаев, например, для систем второго порядка.