Сложные сопротивления. Местные напряжения

6. 1 Понятие о теориях прочности

Нами рассмотрены четыре вида простого нагружения стержней, че­тыре простейших типа их деформаций: растяжение (сжатие), сдвиг, кручение и плоский изгиб. На практике многие детали подвергаются одновременно нескольким простым деформациям, например круче­нию и изгибу, изгибу и сжатию и т.д. Далее рассмотрим расчет на прочность при таком нагружении.

Нагруженные детали механизмов теряют способность выполнять свои функции при наступлении опасного или предельного состояния материала. Для пластичных материалов это состоя­ние связывают с появлением заметных остаточных деформаций, для хрупких — с появлением трещин и началом разрушения. Напряже­ния, соответствующие наступлению опасного состояния материала, зависят от напряженного состояния, обусловленного сово­купностью напряжений для множества площадок, проходящих через рассматриваемую точку. Большинство материалов разрушается по-разному в зависимости от того, являются напряжения растяги­вающими или сжимающими. Имеются напряженные состояния, при которых материал разрушается хрупко, а есть такие, при которых этот же материал пластически деформируется. При одноосном напряженном состоянии, обусловленном растяжением (сжатием), опасное состоя­ние для пластичных материалов возникает при напряжении, равном условному пределу текучести 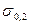для хрупких материалов — пределу прочности 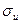. Экспериментально установить числовые значения предельных точек перехода материала в опасное состояние при сложных напряженных состояниях практически невоз­можно из-за технических трудностей ведения испытаний при этих со­стояниях и неисчерпаемости возможных типов таких состояний.

Теории прочности предлагают методы оценки меры опасности любого напряженного состояния. Существуют различные взгляды на причины, вызывающие опасное состояние материала. Одни считают, что опасное состояние наступает при достижении нормальными на­пряжениями предельного значения. Другие рекомендуют за критерий опасного состояния принимать наибольшую относительную дефор­мацию, третьи — величины касательных напряжений. Предлагаемые критерии позволяют сравнивать разнотипные напряженные состоя­ния с опасным состоянием материала при наиболее изученной де­формации — простом растяжении. Напряженные состояния считают равноопасными (равнопрочными), если при пропорциональном увели­чении действующих на тело нагрузок в одно и то же число раз это приводит к опасному состоянию материала. Сравнение напряженных состоя­ний материала проводят по величине эквивалентного (приведенного) напряжения 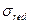при растяжении. Под эквивалентным понимают на­пряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние было равноопасным заданному напряжен­ному состоянию.

Физические процессы, происходящие при переходе в опасные состояния, сильно различаются для пластичных и хрупких материа­лов, поэтому существенно могут различаться и условия перехода в эти состояния.

Рассмотрим несколько классических теорий прочности.

Первая теория прочности (теория наибольших нормальных напря­жений) представляет собой гипотезу о том, что опасное состояние ма­териала при сложном напряженном состоянии наступит тогда, когда наибольшее нормальное напряжение достигнет величины предель­ного напряжения при растяжении. Практическая проверка не под­твердила этой гипотезы, и первая теория прочности в практических расчетах не применяется.

Вторая теория прочности (теория наибольших деформаций) пред­ставляет собой гипотезу, согласно которой при сложном напряжен­ном состоянии опасное состояние материала наступит, если наиболь­шая по абсолютной величине относительная линейная деформация достигнет значения, соответствующего опасному состоянию мате­риала при растяжении или сжатии. Данная гипотеза дает удовлетво­рительное совпадение результатов расчета и эксперимента для хруп­ких материалов.

Третья теория прочности (теория наибольших касательных напря­жений) представляет собой гипотезу, согласно которой прочность материала при сложном напряженном состоянии обеспечена, если наибольшее касательное напряжение не превосходит допускаемого касательного напряжения при растяжении, т.е. 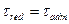. Условие прочности материала по этой гипотезе, выраженное в эквивалентных напряжениях при растяжении, имеет вид

,

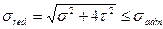где 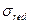— приведенное или эквивалентное нормальное напряжение; 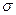, 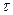— соответственно нормальное и касательное действующие напря­жения; 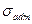— допускаемое напряжение материала при растяжении.

Третья теория прочности широко применяется для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию.

Четвертая теория прочности (энергетическая) представляет со­бой гипотезу о том, что опасное состояние материала при сложном напряженном состоянии возникнет тогда, когда удельная потенци­альная энергия деформации достигнет значения, соответствующего опасному состоянию данного материала при растяжении или сжатии. При расчетах хрупких материалов эта теория неприменима; при ее использовании результаты расчетов хорошо согласуются с опытными данными для пластичных материалов. Условие прочности при ис­пользовании четвертой гипотезы примет вид

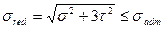
6.2 Изгиб с кручением стержней круглого поперечного сечения

При сложных деформациях в поперечных сечениях стержней действуют одновременно несколько составляющих внутренних сил, например крутящий и изгибающий моменты, поперечная и продоль­ная силы. Расчеты на прочность в этом случае основаны на принципе независимости действия сил с применением выбранной теории проч­ности. Выбор гипотезы прочности определяется прежде всего состоя­нием материала — пластичный или хрупкий.

Решают такие задачи в следующем порядке. Сначала в поперечных сечениях стержня определяют с помощью метода сечений внутрен­ние силы. Для определения положения опасного сечения необходимо построить эпюры внутренних сил. Далее определяют нормальные и касательные напряжения от каждой составляющей внутренних сил. Анализируя распределение напряжений по длине стержня, определяют наиболее нагруженное сечение и наиболее нагруженную точку. Для нее составляют условие прочности с помощью выбранной гипотезы.

Деформации изгиба с кручением подвергаются валы различных передаточных механизмов. Расчет валов на прочность при действии указанных деформаций называют расчетом на статическую проч­ность по наибольшим усилиям.

На рис. 6.1, а показана схема нагружения, действующая на двухопорный вал. Для удобства расчета пространственную систему внеш­них сил представляют в виде сил, вызывающих одновременно изгиб в вертикальной ( 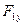, 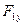) и горизонтальной ( 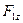, 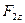) плоскостях. Вал принимается за статически определимый стержень (рис. 6.1, б). Соот­ветственно реакции опор определяют в виде составляющих, действую­щих в вертикальной ( 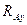, 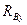) и горизонтальной ( 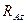, 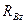) плоскостях.

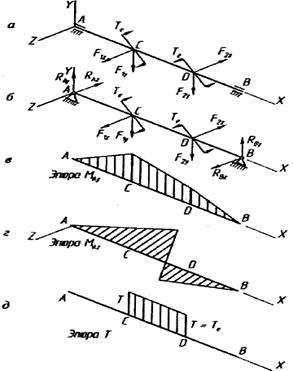
Рис. 6.1

На участке вала CD в поперечных сечениях действует крутящий момент 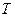равный внешним скручивающим моментам 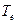. Под дейст­вием приложенной нагрузки в сечениях возникают нормальные от изгиба и касательные от изгиба и кручения напряжения. Величиной касательных напряжений от изгиба пренебрегают, так как она незна­чительна по сравнению с величиной касательных напряжений от кру­чения.

Используя принцип независимости действия сил, строим эпюры изгибающих моментов от вертикальных (рис. 6.1, в) и горизонталь­ных (рис. 6.1, г) сил, а также эпюру крутящих моментов (рис. 6.1, д). При сравнении построенных эпюр видно, что наиболее опасным яв­ляется сечение, проходящее через точку С. В этом поперечном сече­нии помимо крутящего действует и изгибающий момент, который определяется так:

.

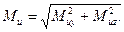Известно, что максимальные нормальные напряжения при изги­бе будут в крайних волокнах и равны:

,

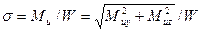где 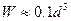— осевой момент сопротивления сечения в виде круга диаметром d.

Наибольшие касательные напряжения при кручении возникают в наиболее удаленных от центра точках сечения и определяются так:

,

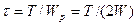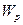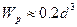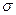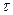где — полярный момент сопротивления сечения; для круга . Подставив значения и в соответствующие выражения для третьей и четвертой теории прочности, за­пишем условия прочности вала при использовании соответственно третьей и четвертой гипотезы прочности:

,

,

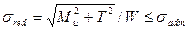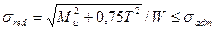где 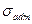— допускаемое напряжение материала вала при растяжении.

Из последних выражений можно найти значение осевого мо­мента сопротивления поперечного сечения вала:

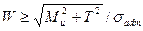или ,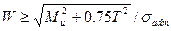

а затем диаметр вала: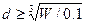

6.3 Концентрация напряжений

Напряжения при растяжении (сжатии), изгибе, кручении и слож­ных деформациях, определяемые по рассмотренным выше зависимо­стям, называют расчетными или номинальными. Экспериментально установлено, что в местах приложения сил, ослабления поперечного сечения отверстиями или выточками, в местах резкого изменения пло­щади поперечного сечения действительные напряжения больше рас­четных. Различие действительных и расчетных напряжений наблюда­ется в ограниченной зоне, т.е. носит местный характер, поэтому и сами напряжения в этой зоне называются местными напряжениями.

Возникновение больших местных напряжений в местах наруше­ния правильной цилиндрической или призматической формы стержня называется концентрацией напряжений. Выточки, отверстия, резкие изменения площади поперечного сечения и другие очаги концентра­ции напряжений называют концентраторами напряжений.

Так, при растяжении полосы (рис. 6.2, а—в) силами 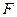в сечениях k -k напряжения равны номинальным: 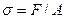, где 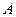— площадь по­перечного сечения полосы. При наличии в пластине отверстия (рис. 6.2, б) или выточки (рис. 6.2, в) распределение напряжений изменяется: у краев отверстия и выточки напряжения максимальны (σmax) и много больше расчетных. Подобное можно наблюдать при изгибе (рис. 6.3, а, когда 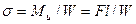, a .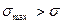

Количественной мерой концентрации напряжений служит коэф­фициент концентрации напряжений. Различают теоретический и эф­фективный коэффициенты концентрации.

Теоретический коэффициент концентрации 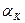равен отношению наибольшего местного напряжения 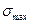в сечении к расчетному на­пряжению σ в этом сечении, т.е. 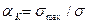. Наибольшие напряже­ния σmах в местах концентрации определяют экспериментально или рассчитывают с помощью методов теории упругости. Значение теоре­тического коэффициента концентрации зависит от вида и размера концентратора и может достигать трех и более. При определении αк не учитывают влияние свойств материала, в частности чувствитель­ность материала к наличию концентраторов. Значения коэффициента αк определены для большинства встречающихся типовых конструк­тивных элементов, они приводятся в справочной литературе в виде таблиц и графиков.

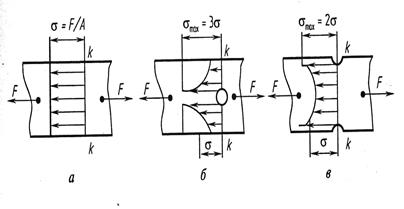
Рис. 6.2

Концентрация напряжений по-разному влияет на прочность конструктивных элементов в зависимости от свойств материала и ха­рактера нагружения. Это учитывается с помощью эффективного коэффициента концентрации 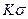. При статическом нагружении 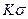оп­ределяется как отношение предела прочности 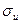образцов без концентраторов к пределу прочности σик образцов, имеющих задан­ный концентратор, т.е. 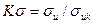. Для пластичных материалов при статических нагрузках концентрация напряжений практически не влияет на прочность. Несущая способность конструкции сохраняется благодаря местной пластической деформации без образования тре­щин в зоне повышенных напряжений. Для пластичных материалов можно считать 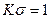и не учитывать концентрацию напряжений при статическом нагружении. Для хрупких материалов значение коэффи­циента 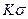приближается к значению теоретического коэффициента концентрации 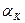. Детали из хрупких материалов при наличии кон­центрации напряжений рассчитывают на прочность по пониженным допускаемым напряжениям 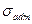. Снижение допускаемого напряже­ния 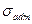пропорционально эффективному коэффициенту концен­трации напряжений .

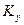Концентрация напряжений обязательно должна учитываться в расчетах на прочность при действии переменных нагрузок.

Для уменьшения концентрации напряжений необходимо:

применять плавные переходы, называемые галтелями, при рез­ком изменении размеров поперечного сечения (рис. 6.3, б);

заменять прорези полукруглыми выточками; увеличивать ра­диусы закруглений галтелей и выточек;

заменять круглые отверстия эллиптическими, вытянутыми вдоль оси стержня;

располагать необходимые отверстия в зоне пониженных напря­жений и т.д.

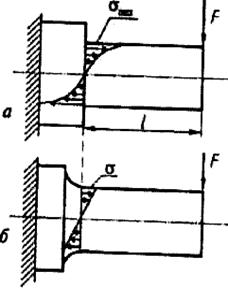
Рис. 6.3

6.4 Контактные напряжения

Большие местные напряжения возникают в местах соприкосно­вения действующих друг на друга тел. Напряжения в месте соприкос­новения двух прижатых друг к другу тел называют контактными. В месте соприкосновения тел вследствие деформации материала об­разуется площадка контакта.

По контактным напряжениям рассчитывают фрикционные и зубчатые передачи, элементы кулачковых механизмов. Определе­ние контактных напряжений при малых размерах площадок контакта для тел различной конфигурации (контактная задача) рассматривает­ся в теории упругости. Расчет базируется на следующих допущениях:

· в месте контакта возникают только упругие деформации;

· поверхности соприкасающихся тел идеально гладкие;

· силы давления, распределенные по площадке контакта, нормальны к поверхности контакта;

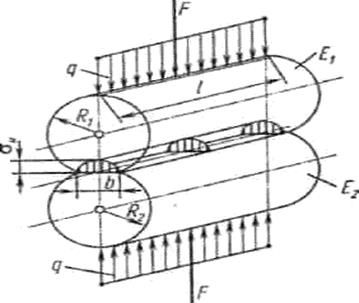
Рис. 6.4

• на площадке контакта возникают только нормальные напряжения.

При размерах площадок контакта, малых по сравнению с общей поверхностью соприкасающихся тел, для определения контактных напряжений используют зависимости, полученные Г. Герцем. На­пряжения в месте контакта зависят от геометрии соприкасающихся тел. Приведем без вывода расчетные формулы для случая сжатия двух цилиндров (рис. 6.4) радиусам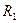и и 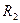и длиной 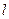по образующей. Считают, что сила прижатия F передается через узкую площадку кон­такта шириной 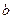и длиной 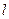. Возникающие на площадке нормальные напряжения распределяются по ее ширине в эллиптической зависи­мости, достигая наибольшего значения в точках оси площадки. Как показал Г. Герц, величина наибольших контактных напряжений

,

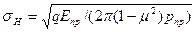где 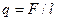— удельная (на единицу длины) нагрузка; 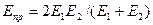- приведенный модуль упругости материалов цилиндров; 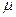— коэффициент Пуассона; 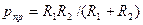- при­веденный радиус кривизны цилиндров; знак « - » берут в случае кон­такта выпуклой поверхности радиусом 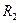с вогнутой поверхностью радиусом 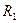. Для материалов с коэффициентом Пуассона 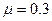вы­ражение для 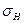примет вид:

.

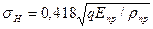Из формулы следует, что контактные напряжения не явля­ются линейной функцией сжимающей силы 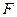и зависят от модуля уп­ругости материала. Они меняются медленнее, чем сама сила, что свя­зано с изменением ширины площадки контакта.

Если размеры площадки контакта соприкасающихся тел значи­тельны и сопоставимы с радиусом кривизны соприкасающихся по­верхностей, имеет место деформация смятия. Например, деформацию смятия рассматривают при определении контактных напряжений ме­жду боковой поверхностью заклепки, болта и цилиндрической по­верхностью отверстия. Считают, что напряжения смятия распределены по площадке контакта равномерно, перпендикулярны к ней и определяются следующим образом:

,

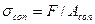где 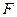— сила прижатия контактирующих тел; 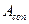— площадь смятия.