СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ВЫБОРКИ

Если записать в последовательности измерений все значения величины х в выборке, то получим простой статистический ряд. Такой ряд неудобен для анализа, так как в нем нет последовательности возрастания (или убывания) значений, встречаются и повторяющиеся величины.

Пусть n – это объем выборки.

Признак х₁ появился m₁ раз

х₂ появился m₂ раз

……………………

x_k появился m_k раз

Значения признака х₁, х₂, …, х_k – это варианты.

Последовательность вариант, записанных в возрастающем порядке называется вариационным (или ранжированным) рядом.

m₁, m₂, ..., m_k – это частоты появления признака

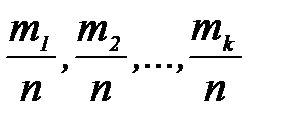- это относительные частоты появления признака или вероятности:

…,

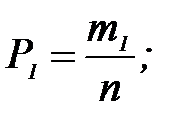
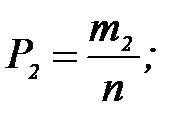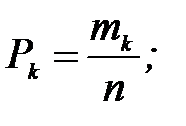
Причем: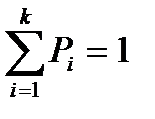

Дискретный вариационный ряд представляют в виде таблицы, которая называется статистическим дискретным рядом распределения.

х	х1	х2	…	xi	…	xk
m	m1	m2	…	mi	…	mk
			…		…

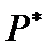
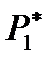
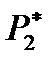
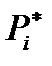
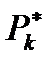
В этом случае строится полигон: по оси абцисс откладывают значения вариант х_i а по оси ординат – значения частот m_i (или относительных частот 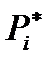). Строится ломанная, которая называется полигоном частот (или относительных частот):

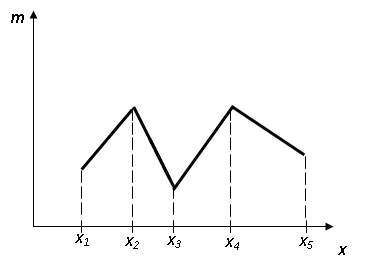
Полигон частот

Непрерывный вариационный рядпредставляют в виде таблицы, которая называется статистическим интервальным рядом распределения.

Интервал	х0- х1	х1- х2	…	xi-1 -xi	…	xk-1- xk
m	m1	m2	…	mi	…	mk
			…		…

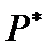
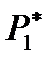
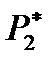
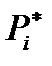
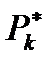
В этом случае строится гистограмма. По оси абцисс откладываются интервалы длиной Δх (Δх – шаг интервала, определяется разностью между максимальным и минимальным значением интервала) и на каждом интервале строят прямоугольник с основанием Δхи высотой 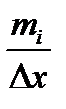(или ).

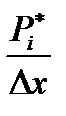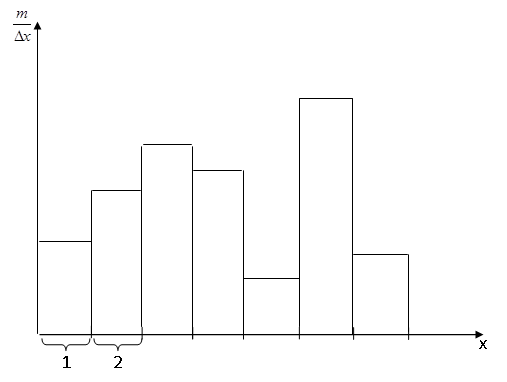
Частоту (или относительную частоту), приходящуюся на единицу интервала называют плотностью частоты (или относительной частоты).

При увеличении числа наблюдений и уменьшении длины (Δх) интервалов верхняя ступенчатая линия гистограммы будет стремиться к плавной кривой и в пределе эта кривая будет графиком плотности вероятности.