ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ И ДОВЕРИТЕЛЬНЫЕ ГРАНИЦЫ

<31 32 333435 36 37 >

Точечная оценка, особенно при малой выборке, может значительно отличаться от истинных параметров генеральной совокупности. Поэтому при небольшом объеме выборки пользуются интервальными оценками.

В этом случае указывается интервал (доверительный интервал или доверительные границы), в котором с определенной (доверительной) вероятностью Р находится истинное значение исследуемой величины (например, среднее значение генеральной совокупности).

Доверительная вероятность Р определяет вероятность, с которой осуществляется неравенство:

(*)

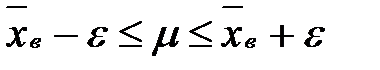где ε –положительное число, характеризующее точность оценки.

Кроме доверительной вероятности используют «противоположенное» понятие – уровень значимости β:

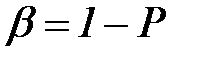
Он выражает вероятность непопадания истинного значения исследуемой величины в доверительный интервал.

Наиболее часто в медицине доверительная вероятность Р принимается равной: 0,95; 0,99 и 0,999.

Если генеральная совокупность распределена по нормальному закону, тогда в неравенстве (*):

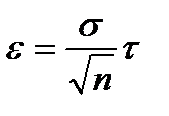
Для нахождения τ используются специальные таблицы Ф-функции.

Тогда доверительный интервал для оценки математического ожидания нормального распределения определится неравенством:

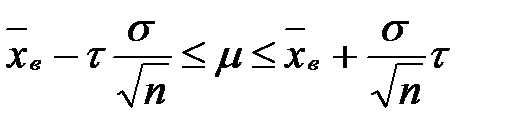
ИНТЕРВАЛЬНАЯ ОЦЕНКА ПРИ МАЛОЙ ВЫБОРКЕ

При достаточно большом объеме выборки можно сделать вполне надёжные заключения о параметрах генеральной совокупности. Однако на практике часто имеют дело с выборками небольшого объема (n<30). Кроме того, почти всегда оказывается неизвестной генеральная дисперсия.

Имея выборку, можно найти лишь исправленную выборочную дисперсию S² и выборочную среднюю 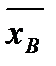. Выразим отклонение выборочного среднего от генерального через S и некоторый параметр t.

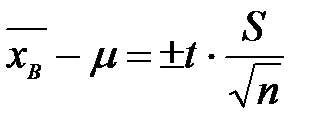или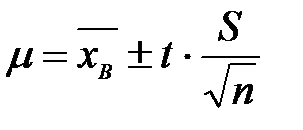

Или представим это в виде интервала:

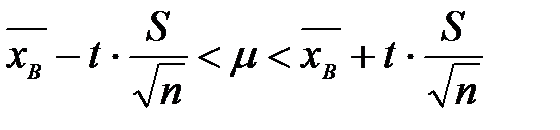
где t- коэффициент Стьюдента, который находится по таблицам, согласно заданному объему выборки и доверительной вероятности (приложение 4).

<31 32 333435 36 37 >

Дата добавления: 2016-06-05; просмотров: 2017;