Выборочная средняя арифметическая величина
Средняя величина, вычисленная на основании ряда чисел, каждое из которых встречается один раз, называется простойсредней арифметической:
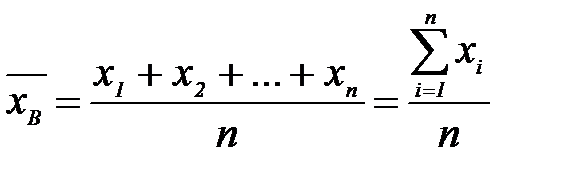
Если значение признака х1 появилось m1 раз
х2 появилось m2 раз
…………………………………
xk появилось mk раз
причем m1+m2+…+mk=n, то вычисляется взвешенная средняя арифметическая:
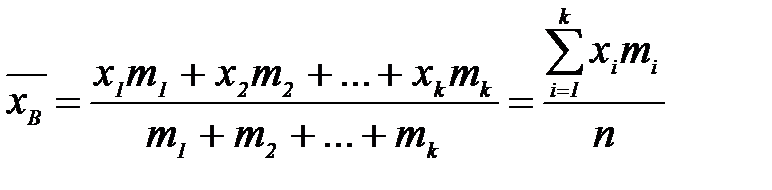
Если при обработке экспериментальных данных составляется интервальный вариационный ряд, то n наблюдавшихся значений величины (х1,х2…xn) группируются в N интервалов с одинаковой длиной интервала Δх. Среднее значение интервала обозначили 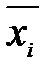 , где i=1,2,3,...,N. Число значений, попавших в интервал обозначается через mi , тогда:
, где i=1,2,3,...,N. Число значений, попавших в интервал обозначается через mi , тогда:
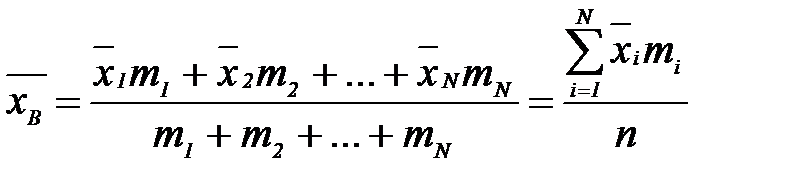
При увеличении объема выборки (n) выборочная средняя стремится к генеральной средней, а это означает, что выборочная средняя есть состоятельная оценка генеральной средней.
2. Модой (Мо) называется наиболее вероятное значение случайной величины или значение величины с наибольшей частотой появления.
3. Медианой(Ме) называется значение варианты, стоящей в центре вариационного ряда, т.е. эта варианта делит вариационный ряд на две равные по числу значений части при условии, что объем выборки есть нечетное число. Если объем выборки четной число то медиана определяется полусуммой двух вариант, стоящих в центре вариационного ряда.
Например:
| х | 3,4 | 3,9 | 4,4 | 4,9 | 5,4 | 5,9 | 6,4 | n=7 |
Ме=4,9
| х | 3,4 | 3,9 | 4,4 | 4,9 | 5,4 | 5,9 | 6,4 | 6,9 | n=8 |
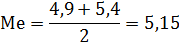
- ВЫБОРОЧНАЯ ДИСПЕРСИЯ И ВЫБОРОЧНОЕ СРЕДНЕЕ
КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ
Выборочной дисперсией ДВ называют среднее арифметическое квадратов отклонения вариант от их среднего значения.
Если все варианты выборки объема n имеют различные значения х1,х2,..,xn, то
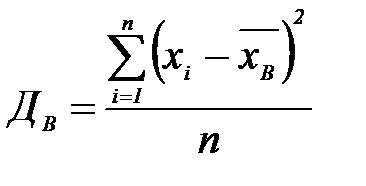 (1)
(1)
Если значение варианты (признака)
х1 появляется m1 раз
х2 появляется m2 раз
…………………………………
xk появляется mk раз,
причем 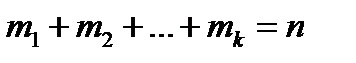 , то
, то
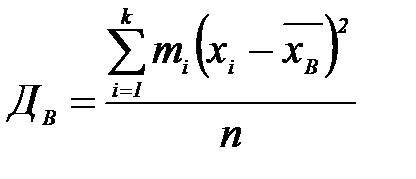 (2)
(2)
Выборочным средним квадратическим отклонением или стандартом отклоненияназывается квадратный корень из выборочной дисперсии:
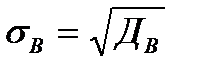
Дисперсию генеральной совокупности нельзя оценить по значениям выборочной дисперсии (это положение можно доказать) поэтому вводится понятие «исправленная дисперсия», которая определяется по формуле:
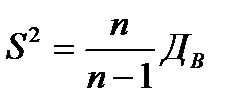
Для формулы (1): 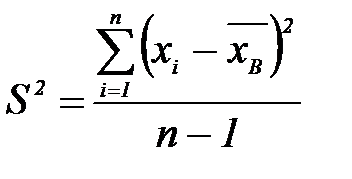
Для формулы (2): 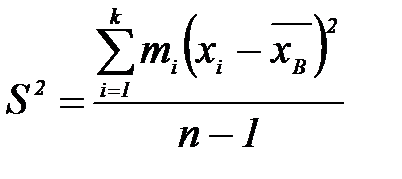
Тогда исправленное среднее квадратическое отклонение 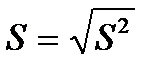
- ДОВЕРИТЕЛЬНЫЕ ВЕРОЯТНОСТИ И УРОВНИ ЗНАЧИМОСТИ.
Дата добавления: 2016-06-05; просмотров: 5688;











