ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Закон распределения непрерывной случайной величины невозможно описать с помощью таблицы, в которой были бы перечислены все возможные значения этой величины и их вероятности. Однако различные области возможных значений случайной величины не являются одинаково вероятными. Для количественной характеристики этого распределения рассматривают не вероятность события X=x, а вероятность события X<x, где x– некоторая текущая переменная. Вероятность этого события зависит от x, т.е. является некоторой функцией распределения случайной величины Xи обозначается F(x):
F(x)=P(X<x)
Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Она существует для всех случайных величин как дискретных, так и непрерывных.
- ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Если рассматривать случайную величину X как случайную точку Xна оси Ox, которая в результате испытания может занять то или иное положение, тогда функция распределения F(x)есть вероятность того, что случайная точка Xв результате испытания попадет левее точки x (рис 2.).
| Х |
| x |
| x |
Рис 2. Геометрическая интерпретация функции распределения.
- ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
1. Как и всякая вероятность, функция распределения не может быть отрицательной и больше единицы:
0 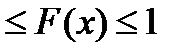
2. Вероятность попадания случайной величины на заданный отрезок (а, b) равна приращению функции распределения на этом отрезке:
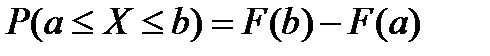
3. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:
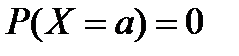
В этом можно убедиться, если рассматривать вероятность попадания случайной величины на заданный отрезок (a,b) при неограниченном уменьшении этого отрезка (b 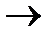 a.) В пределе вместо вероятности попадания случайной величины на отрезок получим вероятность того, что величина примет отдельно взятое значение а:
a.) В пределе вместо вероятности попадания случайной величины на отрезок получим вероятность того, что величина примет отдельно взятое значение а:
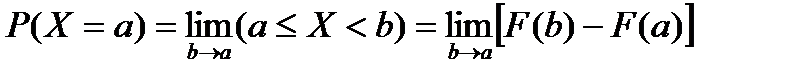
Если функция F(x) в точке а непрерывна, то этот предел равен нулю.
- Если возможные значения случайной величины принадлежат отрезку (a, b), то F(x)=0 при
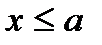 ;
;
F(x)=1 при 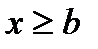 .
.
Пусть 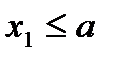 . Тогда событие X<x1 невозможно.
. Тогда событие X<x1 невозможно.
Следовательно, F(x)=P(X<x1)=0.
Пусть 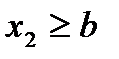 . Тогда событие X<x2 достоверно.
. Тогда событие X<x2 достоверно.
Следовательно, F(x)=P(X<x2)=1.
- ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Вследствие того, что вероятность любого отдельного значения непрерывной случайной величины равна нулю, практической мерой вероятности данного значения x может служить вероятность того, что случайная величина примет значение в бесконечно малом интервале (x, x+  x).
x).
Пусть имеется непрерывная случайная величина X с непрерывной и дифференцируемой функцией распределения F(x). Вычислим вероятность попадания этой случайной величины в интервал (x, x+  x):
x):
P(x<X< x+  x)=F(x, x+
x)=F(x, x+  x)-F(х)
x)-F(х)
Рассмотрим отношение этой вероятности к длине интервала  x и будем приближать значение
x и будем приближать значение  x к нулю. В пределе получим производную от функции распределения:
x к нулю. В пределе получим производную от функции распределения:
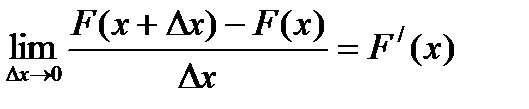
Введем обозначение f(x)= 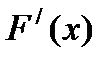 .
.
Функция f(x), являющаяся производной функции распределения, называется плотностью распределения (плотностью вероятности) непрерывной случайной величины X.
Плотность распределения – неотрицательная функция: 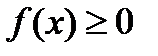 .
.
В противоположность функции распределения плотность распределения существует только для непрерывных случайных величин.
Рассмотрим непрерывную случайную величину Xс плотностью распределения f(x)и бесконечно малый интервал dx, примыкающий к точке x(рис. 3). Вероятность попадания случайной величины X в этот бесконечно малый интервал равна f(x)dx. Величина f(x)dxназывается элементом вероятности. Геометрически это есть площадь прямоугольника, опирающего на отрезок dx.
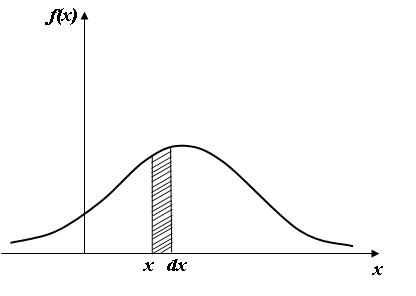
Рис 3. Площадь элементарного прямоугольника, опирающегося на отрезок dx, численно равна элементу вероятности.
Выразим вероятность попадания величины Xна отрезок (a,b) через плотность распределения. Она равна сумме элементов вероятности на всем этом отрезке, т.е. интегралу:
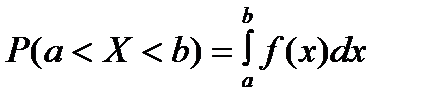 (*)
(*)
Геометрически вероятность попадания величины Xна отрезок (a,b) равна площади, ограниченной кривой f(x), осью абсцисс и перпендикулярами в точках x=a и x=b (Рис. 4)
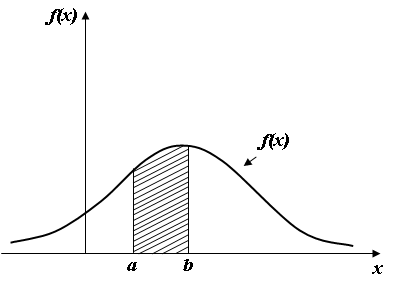
Рис 4. Площадь заштрихованной фигуры численно равна вероятности попадания величины Х на отрезок (а, в).
Выразим функцию распределения через плотность распределения. По определению 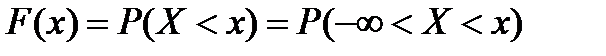 , откуда по формуле (*) имеем:
, откуда по формуле (*) имеем:
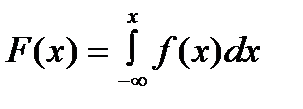 .
.
Геометрически F(x) – это площадь под кривой f(x), расположенная левее x (рис. 5).
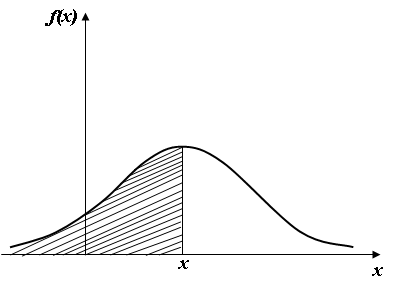
Рис 5. Площадь заштрихованной фигуры численно равна вероятности события Х<x.
Интеграл в бесконечных пределах от плотности распределения равен единице:
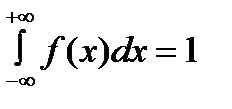 - Это условие нормировки плотности вероятности.
- Это условие нормировки плотности вероятности.
Геометрически это означает, что полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
- ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Закон распределения случайной величины представляет собой некоторую функцию, которая полностью описывает случайную величину с вероятностной точки зрения. Однако при решении многих практических задач нет необходимости характеризовать случайную величину полностью, исчерпывающим образом. Во многих случаях достаточно бывает указать отдельные числовые параметры, в определенной степени характеризующие наиболее существенные особенности распределения случайной величины: например, какое-то среднее значение, около которого группируются возможные значения случайной величины; какое-либо число, характеризующее степень разбросанности этих значений относительно среднего и т.д.
Такие характеристики, которые в сжатой форме выражают наиболее существенные особенности распределения, называют числовыми характеристиками случайной величины. К их числу относятся математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическим ожиданием дискретной случайной величины Xназывается сумма произведений всех возможных значений случайной величины Xна вероятности этих значений.
Математическое ожидание обозначают М(Х)илиμ:
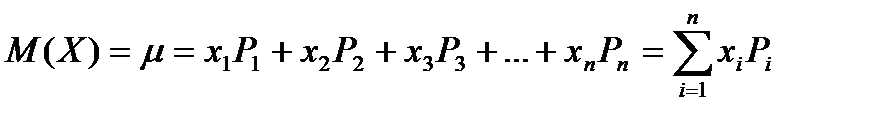
Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины:
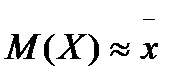
Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [a,b], называют величину определенного интеграла:
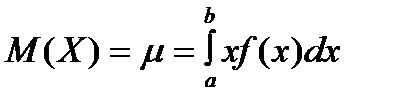 ,
,
где х – непрерывно изменяющаяся случайная величина,
f(x)dx – элемент вероятности.
Если возможные значения х принадлежат всей оси Ох, то
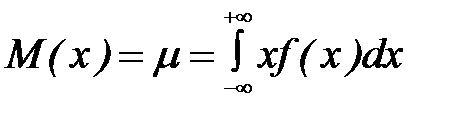 .
.
- СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
- Математическое ожидание постоянной величины С равно этой постоянной: М(С)=С.
- Постоянный множитель С можно выносить за знак математического ожидания: М(СХ)=СМ(Х).
- Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий:
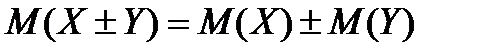
- Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
М(ХY)=M(X)·M(Y)
Математическое ожидание характеризуетположение случайной величины на числовой оси, т.е. указывает некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.
Кроме математического ожидания на практике иногда применяют и другие характеристики положения – модуи медиану случайной величины.
Модой (Мо) называется наиболее вероятное значение случайной величины или значение величины с наибольшей частотой появления.
Если многоугольник распределения (кривая распределения) имеет более одного максимума, распределение называют соответственно двумодальным или многомодальным .
В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, когда распределение является симметричным и модальным (т.е. имеет моду) и существует математическое ожидание, то оно совпадает с модой и центром симметрии распределения.
Медианой(Ме) называется значение варианты, стоящей в центре вариационного ряда, т.е. эта варианта делит вариационный ряд на две равные по числу значений части при условии, что объем выборки есть нечетное число. Если объем выборки четной число то медиана определяется полусуммой двух вариант, стоящих в центре вариационного ряда.
Например:
| х | 3,4 | 3,9 | 4,4 | 4,9 | 5,4 | 5,9 | 6,4 | n=7 |
Ме=4,9
| х | 3,4 | 3,9 | 4,4 | 4,9 | 5,4 | 5,9 | 6,4 | 6,9 | n=8 |
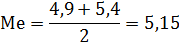
Геометрически медиане соответствует абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
Для краткого описания случайной величины нужно знать степень рассеяния (разброса) ее значений около математического ожидания. Для оценки рассеяния проще всего было бы вычислить все возможные отклонения случайной величины от ее математического ожидания и затем найти их математическое ожидание. Найдем математическое ожидание отклонения:
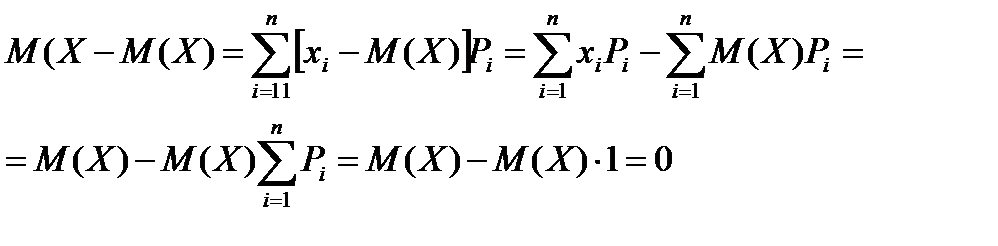
Итак, математическое ожидание отклонения равно нулю. Поэтому величину рассеяния случайной величины относительно ее математического ожидания определяют с помощью числовой характеристики, называемой дисперсией.
Дисперсией дискретной случайной величины называют математическое ожидание квадрата разности случайной величины Х и ее математического ожидания М(Х):
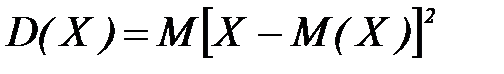 .
.
Дисперсию обозначают Д(X), или 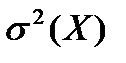 , или
, или 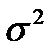 .
.
Для дискретной случайной величины дисперсия равна сумме произведений квадратов отклонений значений случайной величины от ее математического ожидания на соответствующую вероятность:
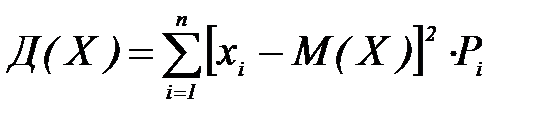 .
.
Дисперсией непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,в], называют величину определенного интеграла:
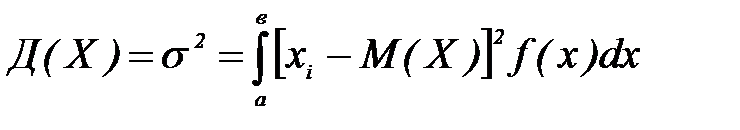 ,
,
где f(x) – плотность вероятности.
Если возможные значения случайной величины принадлежат всей оси Ох, то дисперсия равна:
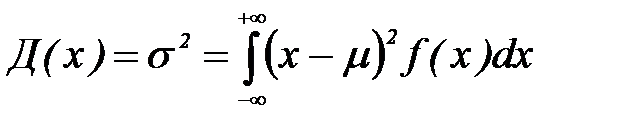 .
.
- СВОЙСТВА ДИСПЕРСИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1. Дисперсия постоянной величины С равна нулю:
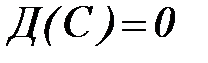 .
.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
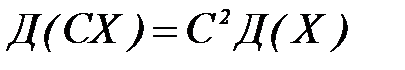 .
.
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
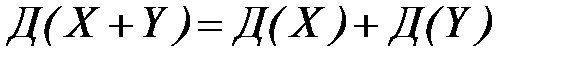 .
.
4. Дисперсия разности двух независимых случайных величин Х и У равна сумме их дисперсий:
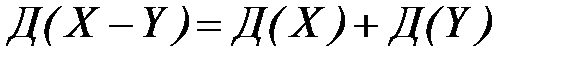
5. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:
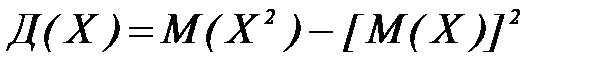 .
.
- СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ
Дисперсия имеет размерность квадрата случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, используют среднее квадратическое отклонение.
Средним квадратическим отклонением случайной величины называют корень квадратный из её дисперсии:
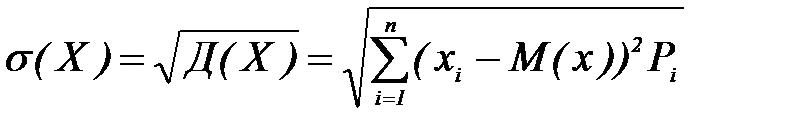 .
.
- НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
Большая часть встречающихся на практике случайных величин подчиняется нескольким законам распределения. Для дискретных случайных величин – это распределение Бернулли (биномиальное), Пуассона, а для непрерывных - Гаусса, Максвелла, Больцмана и другие.
В медико-биологических исследованиях огромную роль играет нормальный закон распределения (закон Гаусса). При действии большого числа случайных факторов, каждый из которых сам по себе оказывает независимо от других незначительное действие на случайную величину, последняя подчиняется закону Гаусса. Так, например, закону Гаусса подчиняются: рост и вес людей; артериальное давление крови, длина сосудов, размеры органов, вес и объем мозга, содержание ферментов у людей и др.
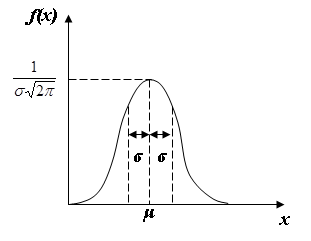
Для нормального распределения, имеющего математическое ожидание μ и среднее квадратическое отклонение σ, плотность распределения имеет вид:
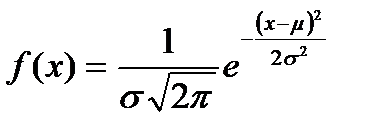 ,
,
а функция распределения вероятности равна:
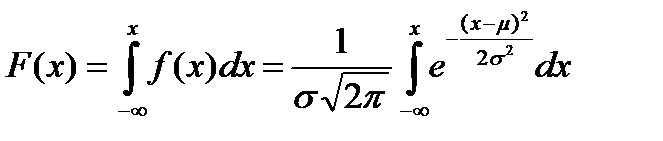 (*)
(*)
Представим закон графически:
Для перехода от двух параметров распределения μ и σ к одному делают замену переменной:
z= 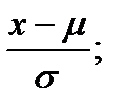 zσ=x-μ; dx=σdz
zσ=x-μ; dx=σdz
Подставив эти значения в функцию распределения (*), получаем:
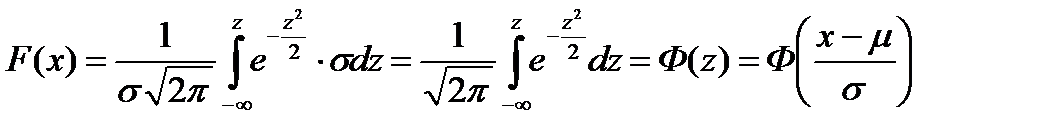
Значение функции Ф(z) обычно находят в специально составленных таблицах. График функции Ф(z) имеет вид:
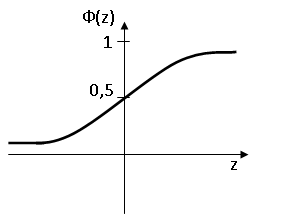
Вероятность того, что значение случайной величины попадает в интервал от а до b, определяется равенством:
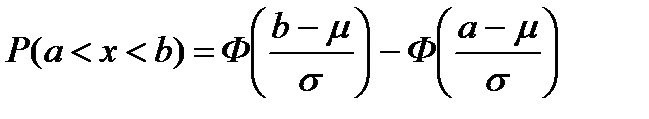
При этом значение функции находят по таблице. Значения функции
Ф(-z)=1-Ф(z)
- СВОЙСТВА НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- Функция плотности нормального распределения определена на всей оси Ох, т.е. каждому значению х соответствует вполне определенное значение функции.
- При всех значениях х функция плотности принимает положительные значения, т.е. нормальная кривая расположена над осью Ох.
- Предел функции плотности при неограниченном возрастании х равен нулю
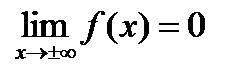 ,
,
т.е. ветви кривой асимптотически приближающей к оси Ох.
- Функция плотности в точке х=μ имеет максимум равный:
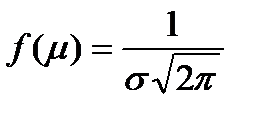
- График функции плотности f(x) симметричен относительно прямой х=μ.
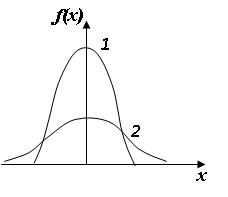
- С ростом σ кривая распределения сжимается к оси абсцисс и растягивается вдоль неё.
σ2>σ1
Для решения задач по нахождению М(х), Д(х) и σ(х), а так же для расчета вероятности попадания случайной величины в заданной интервал для удобства необходимо составлять следующие таблицы:
| Значение случайной величины хi | x1 | х2 | …... | xn | |
| Число случаев mi | m1 | m2 | …... | mn | ∑mi=n |
Вероятность 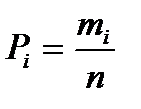
| P1 | P2 | …... | Pn | Условие нормировки ∑Pi=1 |
| Произведения хiРi | x1Р1 | х2Р2 | …... | хnPn | 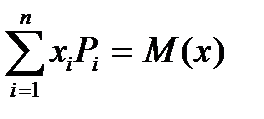
|
Квадраты отклонений сл. величины от мат. ожид. 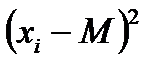
|
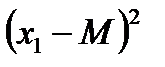
|
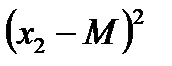
| …... |
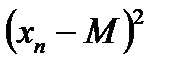
| ___ |
Произведения
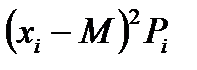
| 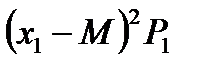
| 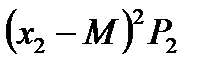
| …... | 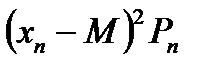
| 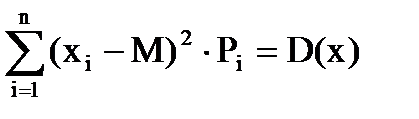
|
Дата добавления: 2016-06-05; просмотров: 8149;











