ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Величина, принимающая те или иные числовые значения в зависимости от различных случайных обстоятельств, называется случайной величиной. Случайными величинами являются: число больных на приеме у врача, число студентов в аудитории, число рождений в городе, продолжительность жизни отдельного человека, температура воздуха и др.

Различают дискретные и непрерывные случайные величины. Случайная величина, принимающая отдельные, изолированные числовые значения, называется дискретнойили прерывной (например, число студентов на лекции, число случаев заболеваний, число родившихся за один день мальчиков и др.).

Случайная величина, принимающая любые значения в определенном интервале, называется непрерывной(например, температура тела больного, продолжительность жизни человека, температура воздуха в течение дня и т.д.).

1. ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Случайные величины обозначают прописными буквами латинского алфавита: X, Y, Z,…, а их возможные значения – соответствующими строчными буквами x, y, z... .

Рассмотрим дискретную случайную величину X с возможными значениями x₁, x₂,…, x_n. Величина Xможет принять каждое из них с некоторой вероятностью. В результате испытания величина X примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий. Обозначим вероятности этих событий буквами P с соответствующими индексами: P(X=x₁)=P₁, P(X=x₂)=P₂,…,P(X=x_n)=P_n.

P₁+P₂+…+P_n= 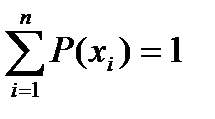- условие нормировки.

Дискретная случайная величина X считается заданной, если перечислены все ее возможные значения и вероятности, с которыми она может принимать эти значения.

Законом распределения дискретной случайной величины называется соответствие между ее возможными значениями и их вероятностями.

Закон распределения дискретной случайной величины может быть представлен в виде таблицы, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:

Такую таблицу называют рядом распределения случайной величины X.

Ряд распределения можно представить графически: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений, и для наглядности полученные точки соединяются отрезками прямых (рис. 1). Такая фигура называется многоугольником распределения. Многоугольник распределения полностью характеризует случайную величину и является одной из форм закона распределения.

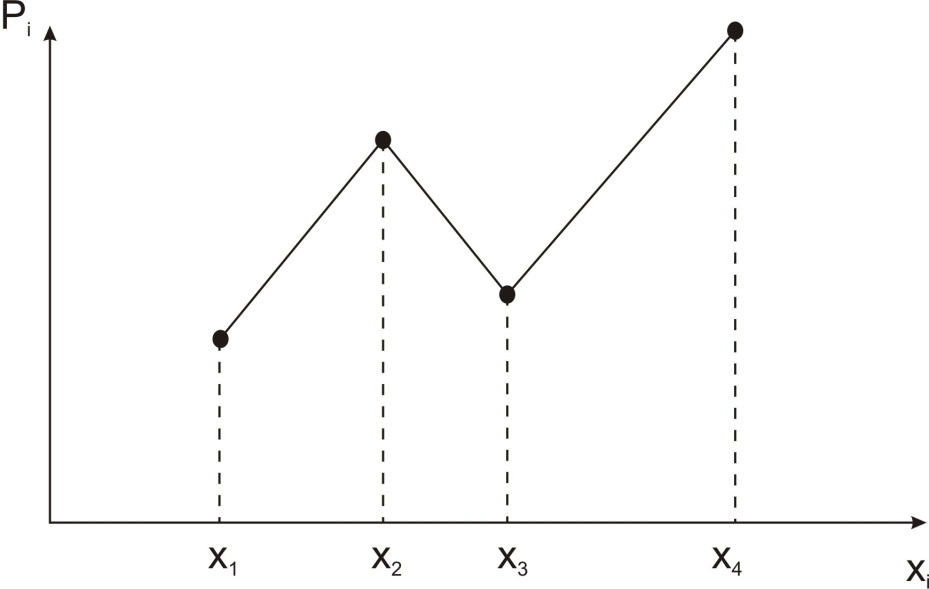
Рис 1. Многоугольник распределения.