Энергетическое распределение тепловых нейтронов описывается спектром Максвелла.

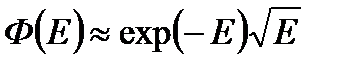
Максвелловское распределение имеет следующие характеристики:

• средняя энергия –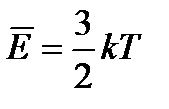

• наиболее вероятная энергия –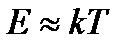

• в результате интенсивного поглощения и утечки тепловых нейтронов время жизни теплового нейтрона конечно и полное тепловое равновесие нейтронов со средой не устанавливается;

• реальный спектр тепловых нейтронов сдвинут от спектра атомов и молекул среды в сторону более высоких энергий;

• вводится понятие стандартизированного теплового нейтрона: E_ст = kT при T = 20,4^oC; E_ст = 0,0253 эВ; (ν_ст=2200 м/с)

Деление реакторного спектра на составляющие является достаточно условным. Кроме того, внутри каждой энергетической области энергетическая зависимость нейтронного потока Ф(r,E) достаточно сложна и ее определение является практически неразрешимой задачей.

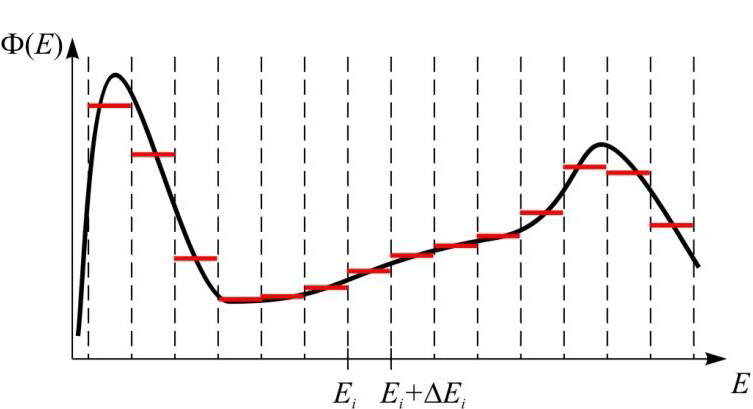
Рассмотрим некоторое энергетическое распределение потока нейтронов, характерное для теплового реактора.

Будем выделять интервалы энергий от E_i до E_i+ΔE_i так, чтобы получить непрерывное разбиение (в общем случае неравномерное) всего энергетического диапазона на группы.

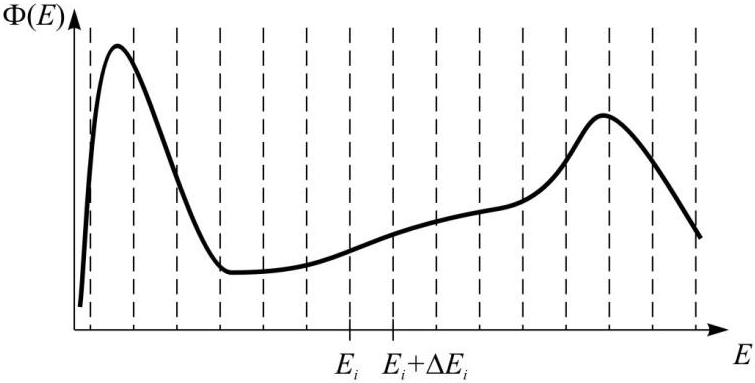
Будем полагать, что внутри каждой энергетической группы нейтронный потокявляется постоянными определяется как среднее значениедля данного энергетического интервала.

При этом внутри каждой группы нейтронырассеиваются без потерь энергии, то есть описываются уравнением диффузии для моноэнергетических нейтронов.

После того как нейтроны испытают достаточное число взаимодействий их энергия изменится дискретно(мгновенно скачком) и нейтрон перейдет в более низкую группу.Переход нейтрона происходит не обязательно в соседнюю группу.Такие переходы продолжаются до тех пор пока нейтрон не попадет в самую нижнюю тепловую группу.

Многогрупповое уравнение.Рассмотрим баланс нейтронов, находящихся в точке r и имеющих энергию E, то есть рассматривает нейтроны в состоянии (r,E). В рамках диффузионного приближения получим уравнение:

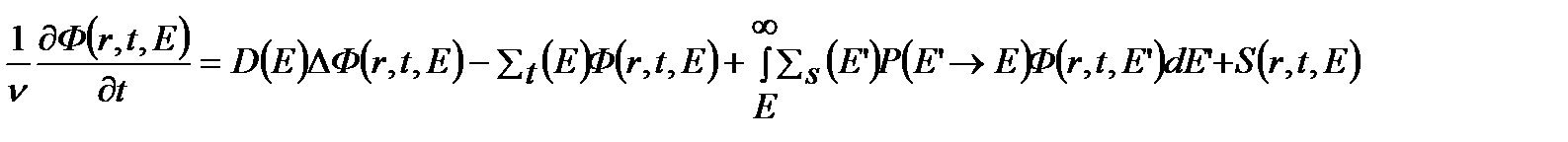(4.2.1)

Где,

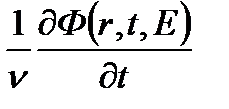- скорость изменения числа нейтронов в состоянии (r,E);

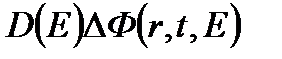- диффузия нейтронов с энергией E;

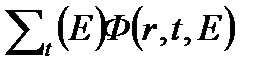- замедление и поглощение нейтронов в точке r, т.е. изменение энергии E;

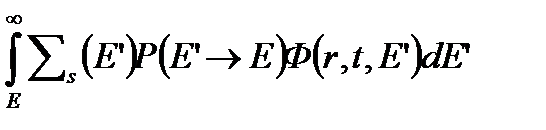- приход нейтронов в состояние (r,E) за счет замедления нейтронов больших энергий в точке r;

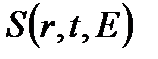- рождение нейтронов в состоянии (r,E) в источнике.

P(E’→E) – вероятность для нейтрона с энергией E’ в результате упругого (el) и неупругого (in) рассеяния замедлится до энергии E;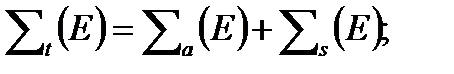

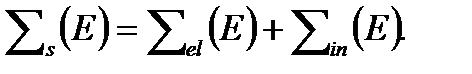
Для стационарного случая будем иметь:

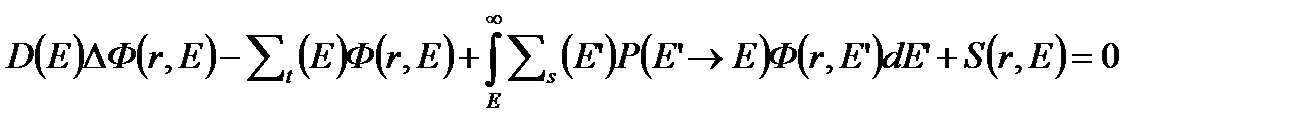(4.2.2)

Здесь, как и в ряде других случаев, удобно сделать замену переменных, введя новую переменную u как 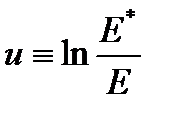. Тогда в новых переменных стационарное уравнение (4.2.2) будет иметь вид:

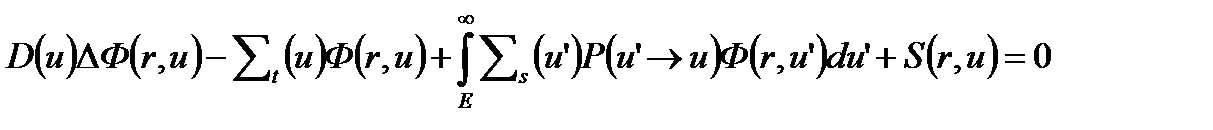(4.2.3)

По аналогии с энергетическим разбиением спектра нейтронов, разобьем шкалу летаргии на конечное число интервалов – m.

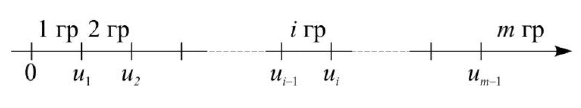
Необходимо обратить внимание на то, что, во-первых, летаргия возрастает с уменьшением энергии. Во-вторых, последняя m-ая группа соответствует тепловым нейтронам.

Заменим исходное уравнение(4.2.3), записанное в переменных летаргии, на систему групповых уравнений. Тогда для любой i-ой группы, внутри которой летаргия изменяется в диапазоне от u_i-1 до u_i получим

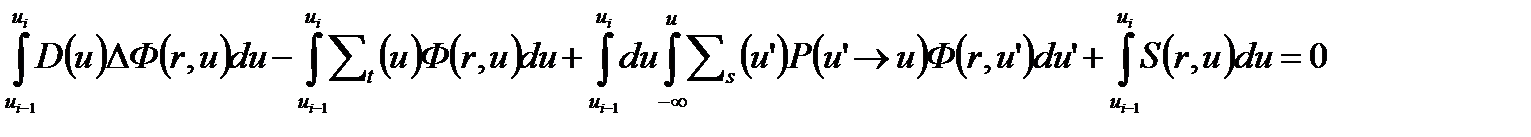(4.2.4)

Левая часть уравнения является суммой четырех интегралов, тогда можно записать I₁-I₂+I₃+I₄=0 (4.2.5)и рассмотреть каждый из них в отдельности.

1) Так как оператор Лапласа влияет только на пространственное изменение потока нейтронов и не зависит от летаргии, то

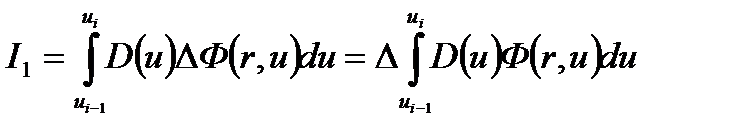(4.2.6)

Последнее выражение умножим и разделим на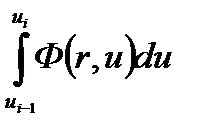

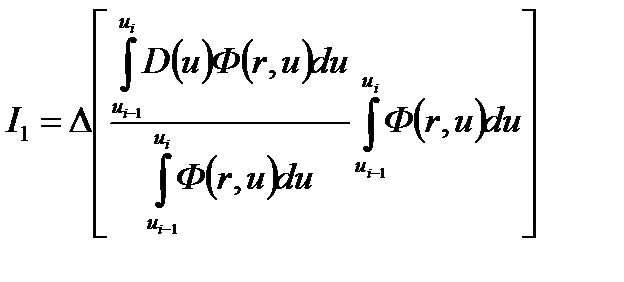(4.2.7)

Полученное отношение интегралов определяет среднее значение коэффициента диффузии (теорема о среднем) для нейтронов с летаргией от u_i-1до u_i или в i-ой группе (D_i).

Оставшийся интеграл определяет интегральный по летаргии (энергии) поток нейтронов в i-ой группе

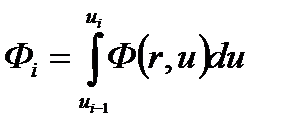(4.2.8)

По-прежнему считаем, что в гомогенной среде коэффициент диффузии не зависит от координаты, окончательно получим для первого интеграла

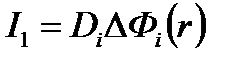(4.2.9)

2) По той же схеме второй интеграл умножим и разделим на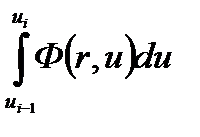

Получим: 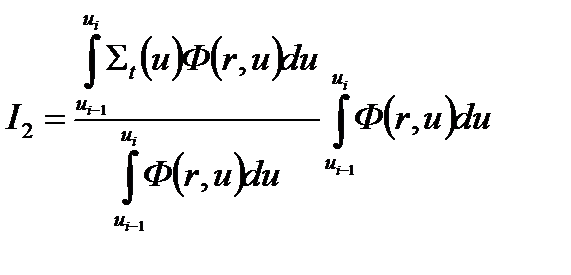(4.2.10)

Отношение интегралов определяет среднее значением макроскопического сечения полного взаимодействия для нейтронов с летаргией от u_i-1 до u_i или в i-ой группе 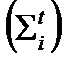. Здесь и далее обозначение вида взаимодействия перенесем в надстрочный индекс.

Для I₂получаем:

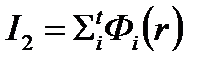(4.2.11)

В макроскопическое сечение полного взаимодействия мы включаем и процессы поглощения, и рассеяния как упругого, так и неупругого 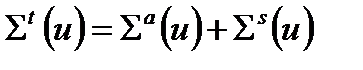. Тогда:

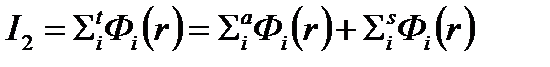(4.2.12)

Первое слагаемое определяет количество поглощенных нейтронов i-ой группы, а 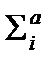– среднегрупповое значение сечения поглощения.

В результате упругих и неупругих рассеяний нейтрон теряет свою энергию. При этом в единичном взаимодействии нейтрон может либо перейти в другую группу, либо остаться внутри i-ой группы.

Тогда сечение рассеяния можно представить как суперпозицию сечения рассеяния, оставляющего нейтрон в i-ой группе 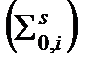и сечения рассеяния, приводящего к переходу нейтрона из i-ой группы в какую-либо другую j-ую группу с большим номером, включая последнюю m-ую тепловую группу.

Последнее сечение будем называть сечением замедления, и определять как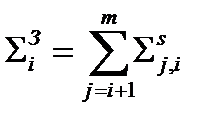

Тогда окончательно для интеграла I₂ будем иметь

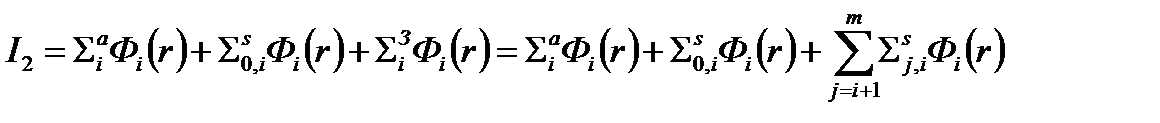(4.2.13)

3) В третьем интеграле заменим порядок интегрирования и учтем, что в среде нет нейтронов с энергией большей, чем энергия источника, что соответствует замене в нижнем пределе интегрирования –¥ на 0. Очевидно, что реальная ситуация с энергетическим распределением нейтронов в реакторе более сложная:

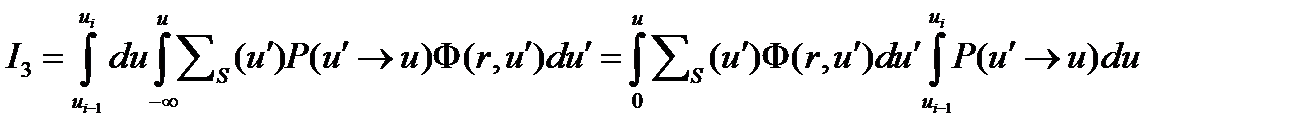(4.2.14)

Разобьем интервал интегрирования 0÷u на три составляющие: 0÷u_i–1; u_i–1÷u_i; u_i÷u. Интервал 0÷u_i–1 характеризует рассеяние нейтронов с летаргиями, меньшими, чем летаргия рассматриваемой i-ой группы. Интервал u_i–1÷u_iописывает рассеяние нейтронов самой i-ой группы. Интервал u_i÷u. характеризует рассеяние нейтронов с летаргиями, большими, чем летаргия рассматриваемой группы, причем все эти нейтроны должны при замедлении попасть в i-ую группу, что противоречит физической сущности замедления.

Интеграл 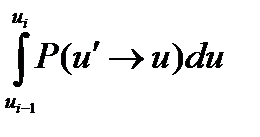есть суммарная вероятность для нейтрона с произвольной летаргией u' замедлится в i-ую группу, тогда:

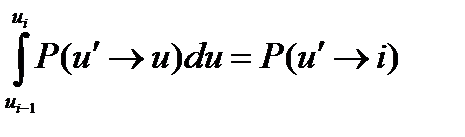
Таким образом

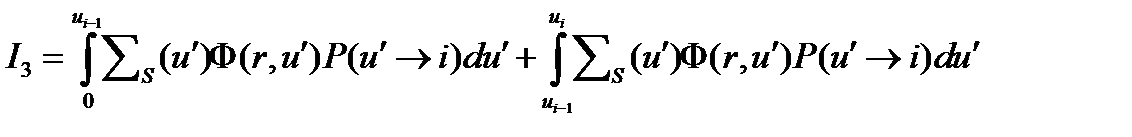(4.2.15)

Применим к интегралу I₃ метод групп, получим

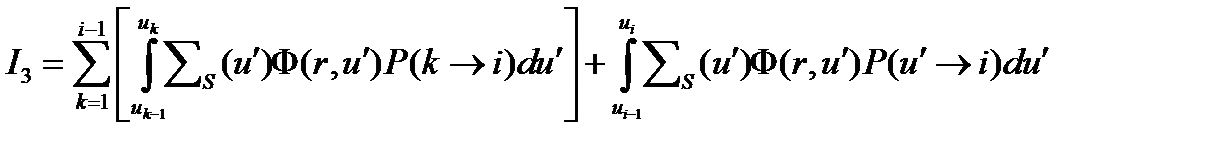(4.2.16)

Всю сумму в первом слагаемом умножим и разделим на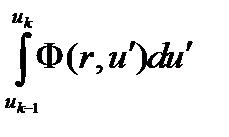

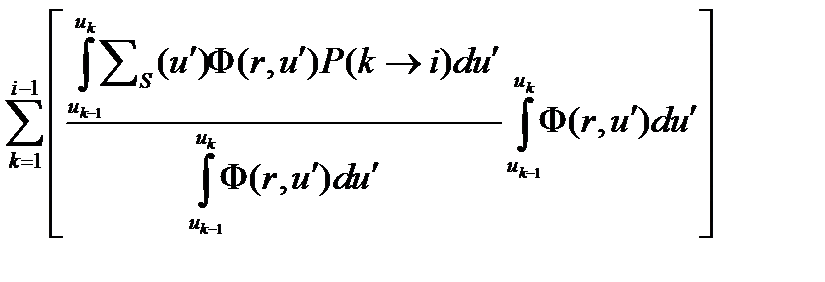
Отношение интегралов есть средняя вероятность нейтрона k-ой группы замедлится в i-ую группу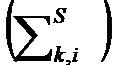

Второй множитель есть интегральный по летаргии поток нейтронов в k-ой группе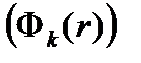

Второе слагаемое в соотношении (4.2.16) для интеграла I₃ умножим и разделим на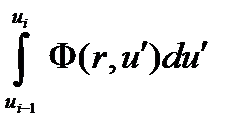

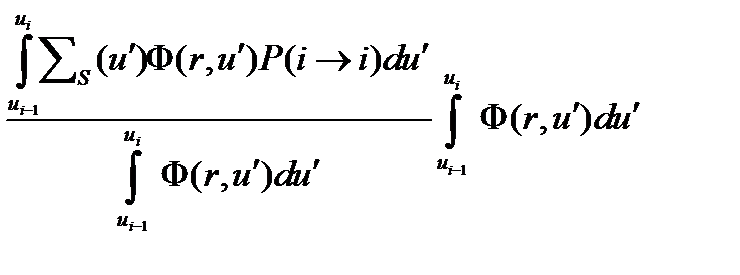
Отношение интегралов есть средняя вероятность для нейтрона остаться в i-ой группе при рассеянии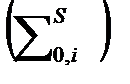

Второй множитель есть интегральный по летаргии поток нейтронов в i-ой группе.

Окончательно для интеграла I₃ получим

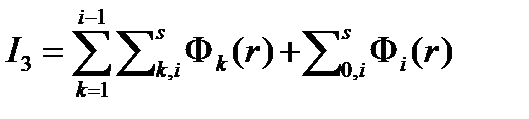(4.2.17)

4) Последний интеграл I₄ характеризует источник.

Рассмотрим случай когда источником является реакция деления. Скорость реакции деления, инициируемой нейтроном с летаргией u' в точке r определится как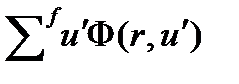

При каждом делении рождается v^f новых нейтронов, причем это количество зависит от энергии нейтрона, вызвавшего деление 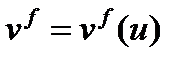Тогда количество нейтронов, образующихся в точке r при делении ядер нейтронами с летаргией u' определится как .

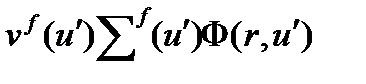Чтобы получить полное число новых нейтронов, образованных в реакции деления, необходимо проинтегрировать полученное соотношение по всему диапазону летаргий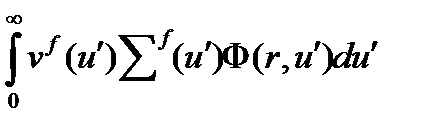

Введем нейтронный спектр деления f(u) в переменных летаргии, то есть долю нейтронов деления имеющих летаргию u, тогда функция источника примет вид

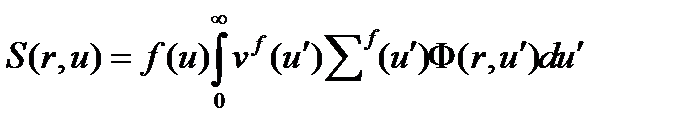
а последний интеграл I₄ получим в виде

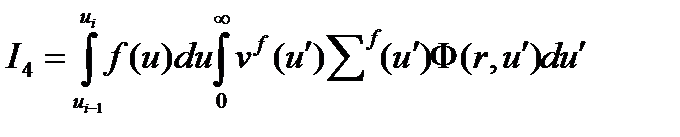
Далее используем много групповой подход

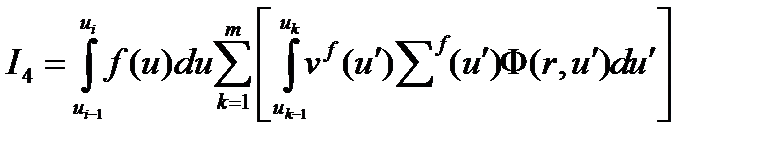
Интеграл под суммой умножим и разделим на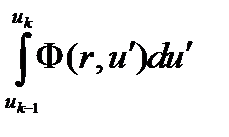

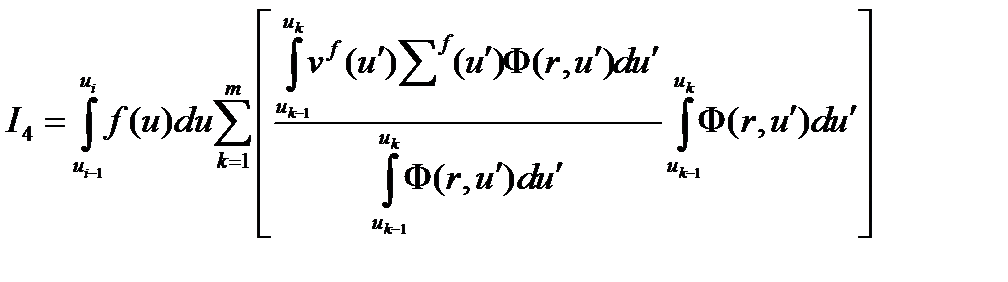
Отношение интегралов есть среднее значение произведения v^få^f для k-ой группы.

Второй множитель есть интегральный по летаргии поток нейтронов в k-ой группе.

Обозначим 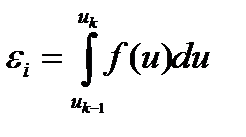– вероятность (долю) нейтронов спектра деления попасть в i-ую группу.

Окончательно для интеграла I₄ получим

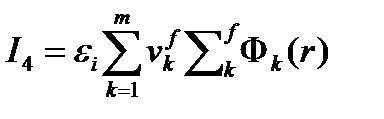(4.2.18)

Соберем все полученные результаты для интегралов I₁, I₂, I₃, I₄ в стационарное уравнение диффузии для i-ой группы

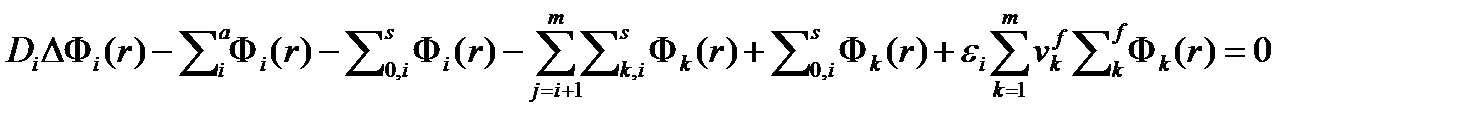(4.2.19)

Введем обозначения:

для макроскопического сечения рассеяния, приводящего к замедлению нейтрона из i-ой группы в j-ую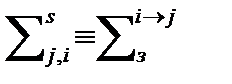

для макроскопического сечения рассеяния, приводящего к замедлению нейтрона из k-ой группы в i-ую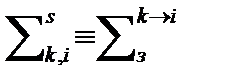

В новых обозначениях и после приведения подобных слагаемых получим

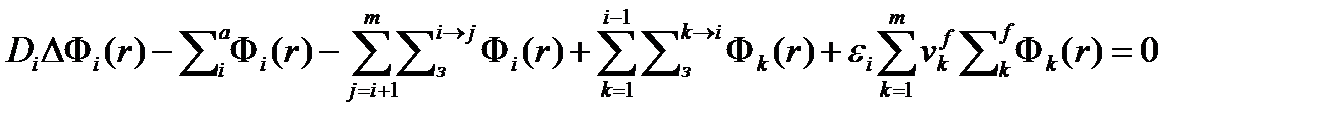(4.2.20)

Определим физический смысл каждого слагаемого, входящего в уравнение (4.2.20):

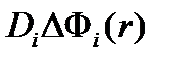– пространственная утечка нейтронов i-ой группы вследствие диффузии в единицу времени из единицы объема вблизи точки r.

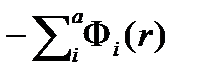– поглощение нейтронов i-ой группы в единицу времени в единице объема вблизи точки r.

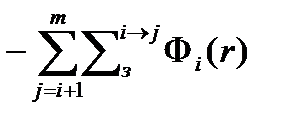– уход нейтронов i-ой группы во все группы с меньшей энергией (большим номером) в единицу времени в единице объема вблизи точки r в результате упругого и неупругого рассеяния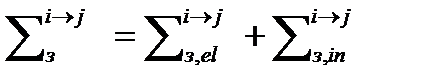

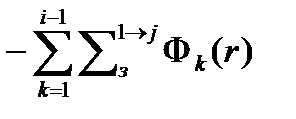- приход нейтронов в i-ую группу из всех других групп с большей энергией (меньшим номером) в единицу времени в единице объема вблизи точки r в результате упругого и неупругого рассеяния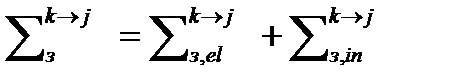

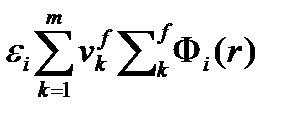– вклад источника нейтронов в i-ую группу в единицу времени в единице объема вблизи точки r.

Система многогрупповых уравнений основана на уравнении диффузии, соответственно, применима в условиях диффузионного приближения: внутри пространственной области с изотропными свойствами вдали от источников, сильных поглотителей и т.д.

При наличии границ раздела сред необходимо записывать граничные условия для каждого уравнения. По-прежнему граничные условия должны обеспечивать непрерывность потоков нейтронов и диффузионных токов на геометрической границе.