Функция ценности нейтронов в многогрупповом приближении

Соответственно, статистический вес нейтронов в таком ЯР

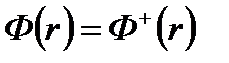
Т.е. максимальную ценность имеют нейтроны в центре ЯР, где Ф максимально. На экстраполированной границе ценность нейтронов равна нулю, т.к. нейтроны, вылетевшие из ЯР, обратно не возвращаются (Ф=0).

Рассмотрим многогрупповое приближение, для которого систему уравнений запишем в уже известном виде

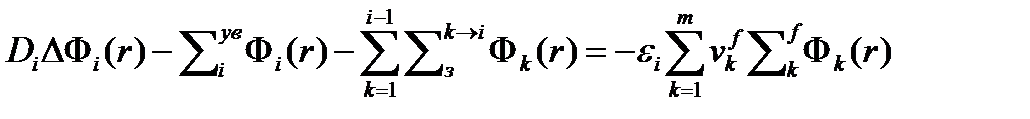(4.3.1)

Левую и правую части этой системы уравнений можно записать в операторном виде: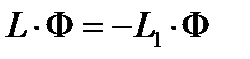

Для левых частей уравнений получим в матричном виде

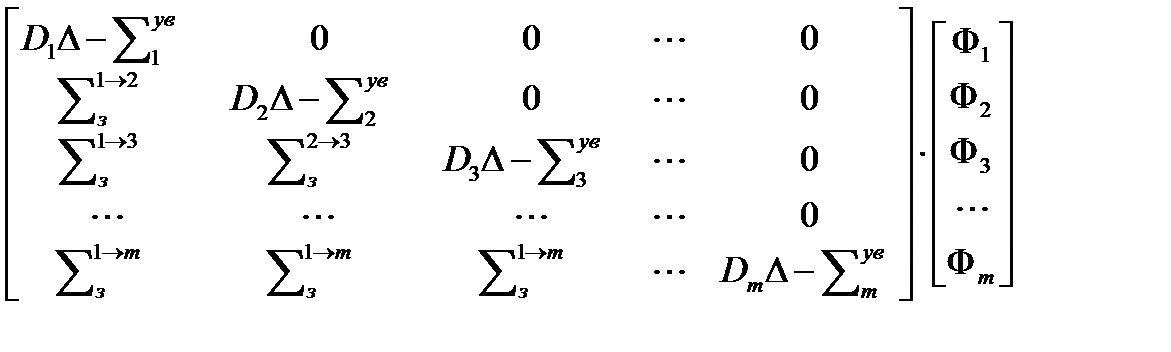
Для правых частей уравнений получим в матричном виде:

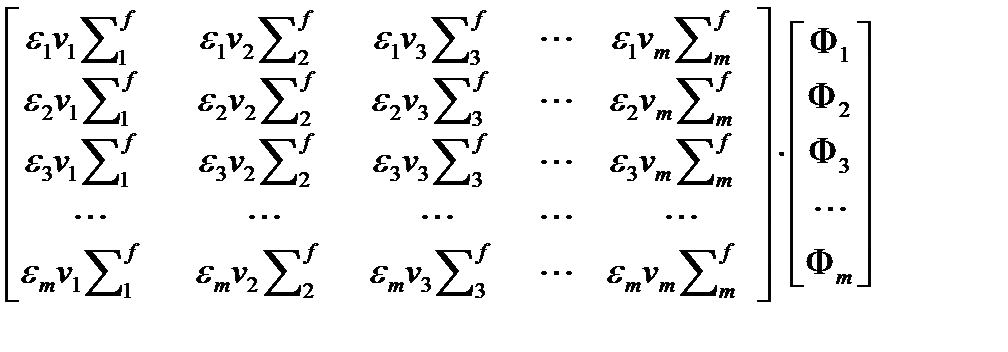
Т.е., вместо системы в дифференциальном виде (4.3.1), получили ту же систему, но записанную в матричном виде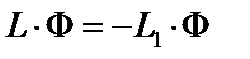

Для получения многогрупповых уравнений для функций ценности нейтронов каждой группу необходимо в матричном уравнении для потоков нейтронов заменить матрицы-операторы на транспонированные комплексно сопряженные матрицы, а функции потоков на сопряженные функции (ценности нейтронов):

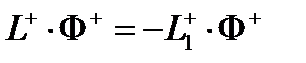
Т.к. наши матрицы-операторы состоят только из действительных элементов, то сопряженные матрицы будут равны транспонированным. Для транспонирования матрицы необходимо поменять местами строки и столбцы.

Для сопряженной матрицы в левой части уравнения для ценностей получим

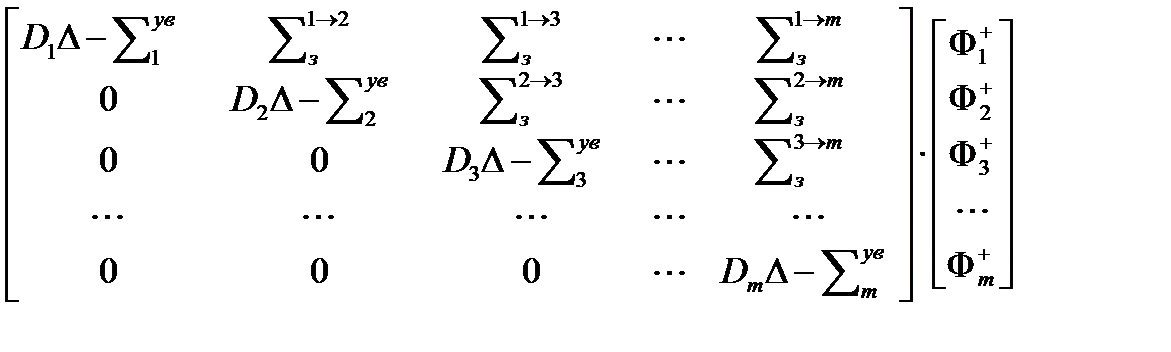
Для сопряженной матрицы в правой части будем иметь

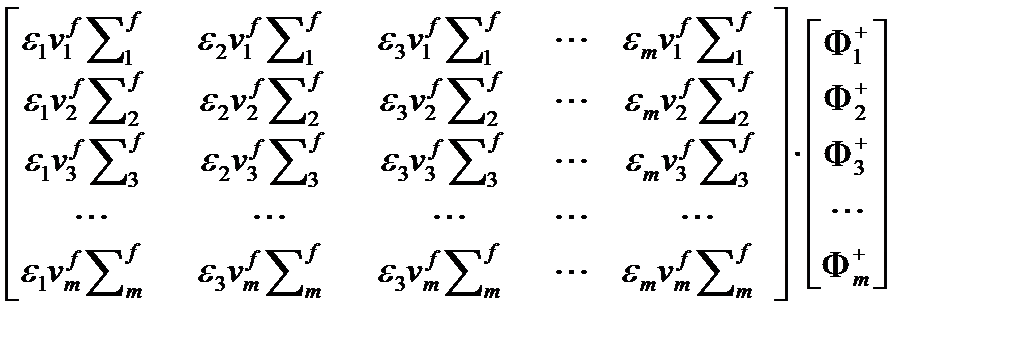
В итоге получаем систему многогрупповых уравнений для групповых функций ценностей нейтронов в дифференциальном виде

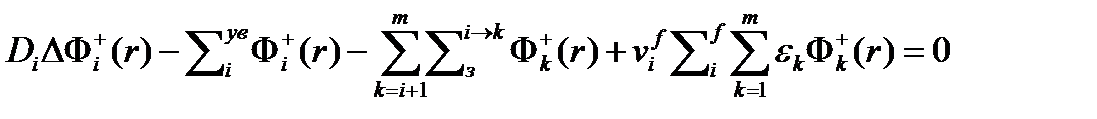
Обозначим 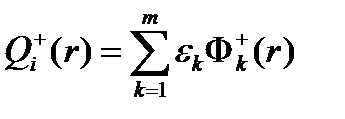– источник ценностей нейтронов.

Тогда, заменив, сечение увода на составляющие (поглощение и замедление) получим

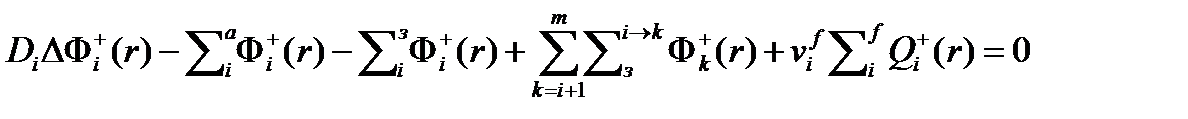
Для критического эквивалентного ЯР, как и в уравнениях для потоков нейтронов, в уравнениях для ценностей будем заменять слагаемое с оператором Лапласа через

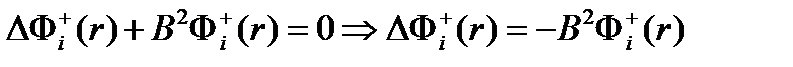
С учетом этого интегрируя уравнения по всему объему ЯР, т.е. переходя от дифференциального распределения функций ценности нейтронов по координате к интегральным ценностям, имеем систему алгебраических уравнений:

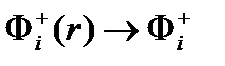
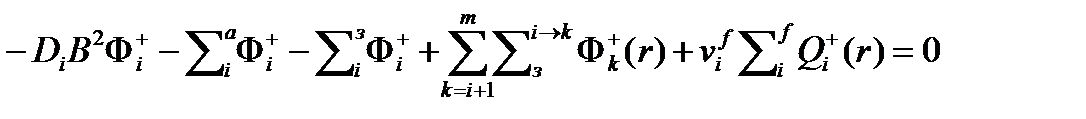
Спектр интегральных по объему ЯР ценностей нейтронов является решением этой системы. Для i-ой группы получим

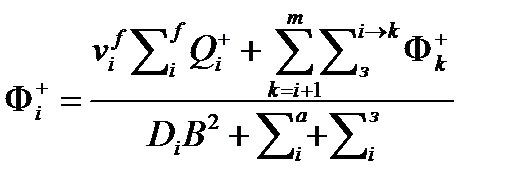
Набор значений 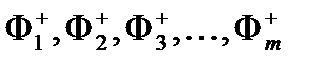как и для потоков нейтронов ищется по аналогии с плотностями потоков нейтронов методом итераций.