Условие критичности для гомогенного голого ядерного реактора конечных размеров. Материальный и геометрический параметры и их величины, их соотношение в реакторе

Расчеты, основанные на одногрупповом приближении, не дают точных результатов для реактора на тепловых нейтронах. Такие расчеты не учитывают потери нейтронов во время замедления. Улучшить результаты можно, если замедлитель не является слишком легким (водородные замедлители исключаются). Здесь для уточнения описания поведения нейтронов во время замедления используется уравнение возраста.

Основная идея заключается в замене источника S в уравнении диффузии на плотность замедления для энергии, соответствующей тепловой.

Число нейтронов деления в 1 см³ в 1 сек, которые замедляются до какой-либо энергии, равно плотности замедления, соответствующей этой энергии.

Если бы во время замедления отсутствовало поглощение, то плотность замедления смогла бы сравняться с величиной q_th (плотность замедления, соответствующая тепловым нейтронам), которая в свою очередь могла бы быть найдена решением уравнения возраста.

В случае относительно слабого поглощения нейтронов плотность замедления можно определить произведением:

φq(τ_th )

где φ – вероятность избежать резонансного захвата для нейтронов возраста τ_th.

Это произведение можно подставить вместо источника в уравнение диффузии.

Таким образом мы полагаем, что источником тепловых нейтронов являются не реакция деления, как в одногрупповой модели, а замедлившиеся до тепловой энергии нейтроны. Очевидно, что такая аппроксимация более соответствует физической системе.

Хотя здесь процесс замедления происходит мгновенно, что является хорошим приближением, так как время диффузии много больше, чем время замедления.

Тогда для реактора, находящегося в критическом состоянии будем иметь стационарное уравнение следующего вида

DΔФ(r) - ΣаФ(r) + Φq(τ,r) = 0 (3.4)

Где DΔФ(r) – диффузия тепловых нейтронов;

ΣаФ(r) – поглощение тепловых нейтронов;

Φq(τ,r) – замедление нейтронов

При этом плотность замедления определяется уравнением возраста:

dq(τ,r)/dτ=Δq(τ,r) (3.5)

Одно из таких условий получается при рассмотрении плотности замедления нейтронов деления, для которых возраст равен нулю, q(0, r).

Для бесконечной размножающей среды, состоящей из замедлителя и делящегося материала, на каждый поглощенный нейтрон будет получатся µηθ быстрых нейтронов следующего поколения, где

µ– коэффициент размножения на быстрых нейтронах;

η– среднее число нейтронов, образующихся при делении;

θ– коэффициент использования тепловых нейтронов.

Тогда число образующихся быстрых нейтронов на каждый тепловой будет равно

µηθ φ/φ=µηθφ/φ=k_∞/φ

Общее число тепловых нейтронов, поглощенных 1 см³ в 1 сек, равноΣaФ. Следовательно, полное число быстрых нейтронов, образующихся в единице объема за единицу времени, равное плотности замедления нейтронов деления, даст соотношение:

q(0,r)=k_∞/φ * Σa Ф(r)

Последнее является условием связи между уравнением диффузии тепловых нейтронов и уравнением возраста.

Плотность замедления, которая определяется уравнением возраста:

dq(τ,r)/dτ=Δq(τ,r) (3.6)

есть функция переменных – возраста и пространственных координат r.

Можно искать решение уравнения возраста путем разделения переменных, то есть положить:

q(τ,r)=T(τ)R(r)

где T(τ) – функция только возраста (или энергии), R(r) – только координат. Выполнив несколько простых преобразований, окончательно получим из уравнения возраста для плотности замедления нейтронов:

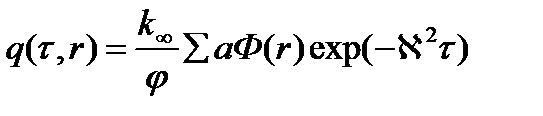(3.7)

Уравнение диффузии для критического гомогенного реактора теперь можно записать в виде:

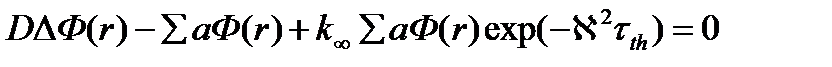
Зная, что нейтронный поток Ф(r) пропорционален функции R(r). Следовательно, функция Ф(r) должна удовлетворять дифференциальному уравнению для R(r), тогда

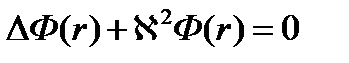
Выразим от сюда ΔФ(r) и подставим в уравнение диффузии

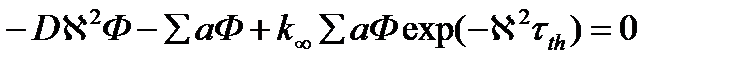
Разделим на Σ_aФ и с учетом L² = D/ Σ_aполучим

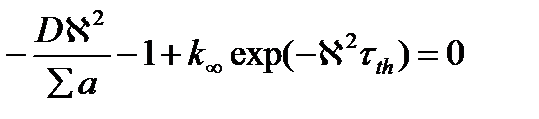
и окончательно:

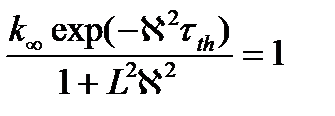(3.8)

Это трансцендентное уравнение называется критическим уравнением.

Уравнение справедливо для гомогенного реактора без отражателя, применимо к тепловым нейтронам с пространственным распределением плотности, определяемым возрастом нейтронов.

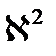– материальный параметр, что подчеркивает его зависимость только от свойств гомогенной среды.

3.2.2 Баланс нейтронов в реакторе конечного размера

Как уже неоднократно отмечалось, различие между реактором бесконечных размеров и реактором конечных размеров заключается в потере нейтронов в результате утечки через границы.

Для бесконечного реактора критическое условие сводится к равенству коэффициента размножения в бесконечной среде единице

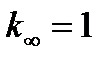
Рассмотрение гомогенного реактора в диффузионно-возрастном приближении привело к появлению двух множителей:

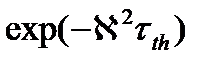и ,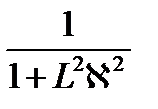

которые учитывают конечность размеров, а соответственно, возможность утечки.

Число тепловых нейтронов, поглощенных в 1 см³ в 1 сек равно

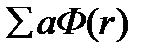
Коэффициент размножения в бесконечной среде k_∞ по определению равен среднему числу тепловых нейтронов, генерируемых в одном поколении нейтронов на каждый поглощенный нейтрон в бесконечной среде.

Тогда для бесконечной среды (при отсутствии утечки) плотность источников тепловых нейтронов равняется

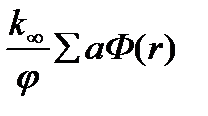
Для среды конечных размеров ту же плотность источников тепловых нейтронов мы определили как плотность замедления умноженную на вероятность избежать резонансного захвата – φq(r,τ) или с учетом решения уравнения возраста

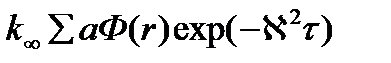
Если плотность источников тепловых нейтронов:

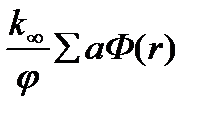- для бесконечной среды;

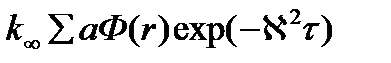– для среды конечных размеров,

то тогда по физическому смыслу это – вероятность того, что нейтрон избежит утечки из реактора (останется в реакторе) конечных размеров в процессе замедления.

Приращение числа нейтронов в 1 см³ за 1 сек вследствие диффузии в элементе объема с центром в точке r равно:

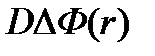
Тогда на оборот, утечка нейтронов в 1 см³ за 1 сек вследствие диффузии из элемента объема с центром в точке r равна:

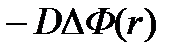
Так как 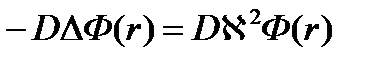,то число тепловых нейтронов, покидающих единицу объема за единицу времени, равно:

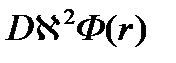
Следовательно, отношение утечки тепловых нейтронов к поглощению тепловых нейтронов:

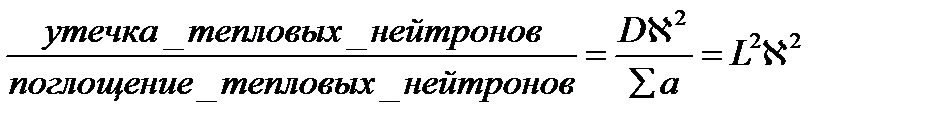
не зависит от координаты, то есть одинаково в любой точке, а соответственно, и в реакторе в целом.

Отсюда получается доля нейтронов, замедленных до тепловой энергии и поглощенных в топливе

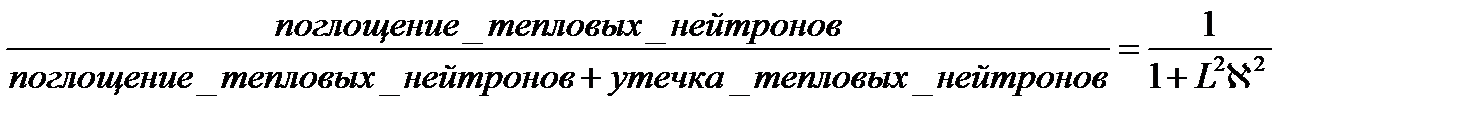
Соответственно, по физическому смыслу величина 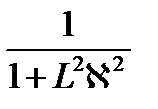это – вероятность того, что тепловой нейтрон избежит утечки при диффузии (останется) в реакторе.

Применимы более короткие названия для введенных вероятностей:

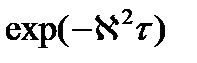– коэффициент утечки быстрых нейтронов;

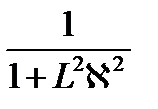– коэффициент утечки тепловых нейтронов.

Таким образом, произведение этих двух коэффициентов является полной вероятностью (P) того, что нейтроны избегут утечки в реакторе конечных размеров за их полный жизненный цикл – от появления как нейтронов деления до захвата в области тепловых энергий.

С учетом полученных вероятностей для реактора конечных размеров условие критичности является более жестким, чем для бесконечной среды.

Коэффициент размножения для бесконечной среды, описывающий изменения количества нейтронов в одном поколении за чет взаимодействия с ядрами среды (в т.ч. деления), необходимо умножить на вероятность избежать утечки за полный жизненный цикл и потребовать равенства 1 уже для этой произведения в целях обеспечения критичности конечного реактора.

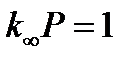
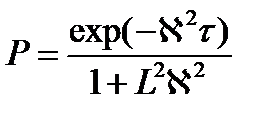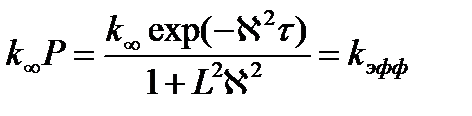Тогда, если , то (3.9)

3.2.3. Критические параметры реактора

Одной из самых важных задач физики реакторов является нахождение критических параметров.

Под критическими параметрами будем понимать совокупность материальных и геометрических характеристик реактора, при обеспечении которых нейтронный поток не меняется во времени.

В общем случае нейтронный поток в гомогенном реакторе конечных размеров описывается нестационарным уравнение диффузии с источником нейтронов в виде плотности замедления для нейтронов тепловых энергий

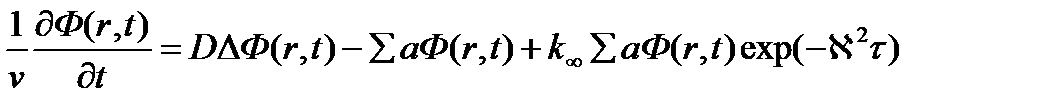(3.10)

Разделим данное уравнение на коэффициент диффузии D, тогда

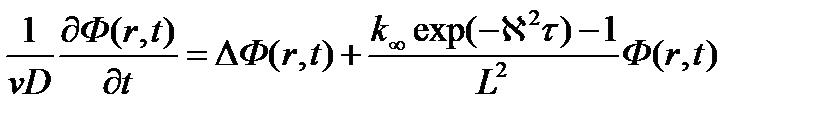
Из критического уравнения имеем

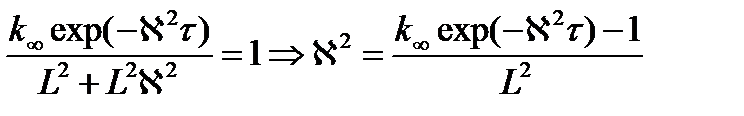
Окончательно получим уравнение в виде

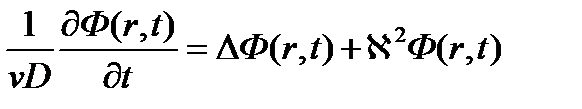
Реактор станет критическим, когда прекратится изменение потока нейтронов во времени. В этом случае данное уравнение станет стационарным

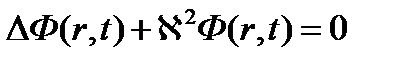(3.11)

Следовательно, если будут найдены условия такого перехода, то эти условия и будут являться условиями критичности реактора.

Таким образом, будем рассматривать полученное нестационарное уравнение в целях поиска условий, при которых функция потока перестанет изменятся во времени.

Предположим, что переменные в функции Ф(r,t) разделяются, тогда функцию потока можно представить в виде

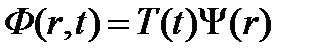
Подставив это выражение в выражение (3.10) и собрав функции зависящие от времени в левой части, а функции от координаты в правой, получим

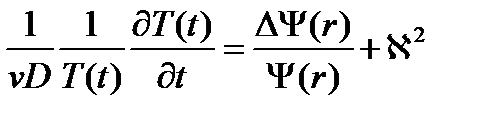(3.12)

Так как правая и левая части уравнения есть функции разных независимых переменных, то тождество возможно, если обе части будут равны какой-либо константе.

У нас нет специальных ограничений на функции T(t) и y(r), поэтому пусть это будут просто константа w, тогда из левой части будем иметь

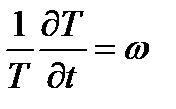
Решение этого уравнения будем иметь в виде .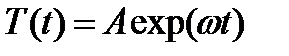

Тогда для функции Ф(r,t) получим 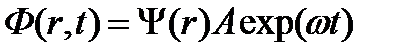и снова подставив в нестационарное уравнение получим:

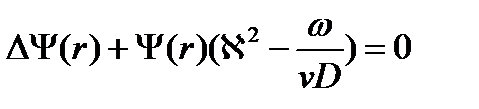
Выражение в скобках обозначим B², тогда

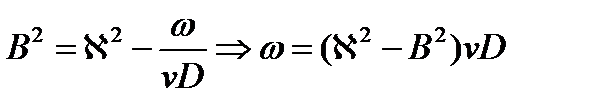
Следовательно, 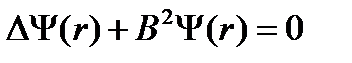.Полученное уравнение относится к дифференциальным уравнениям специального типа, который называется задача Штурма-Лиувилля.

Общее решение для уравнений данного типа представляется в виде разложения искомой функции в ряд

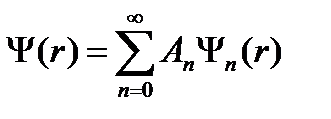
Таким образом, окончательно решение нестационарного уравнения для функции Ф(r,t) будем иметь в виде

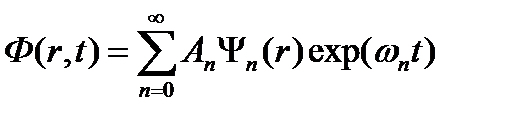
где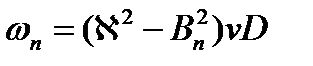

Таким образом, в результате проведенного анализа окончательно получаем:

если 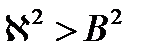,то реактор находится в подкритическом состоянии;

если 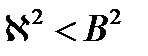,то реактор находится в надкритическом состоянии;

если 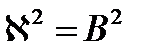,то реактор находится в критическом состоянии.

В обозначении параметра B опустим индекс «0» и будем называть его геометрическим параметром.

Условие критичности: в гомогенном ядерном реакторе без отражателя в диффузионно-возрастном приближении материальный параметр равен геометрическому:

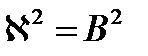
3.3. Критические размеры гомогенных голых реакторов различной геометрии, их геометрические параметры, распределение плотности потока нейтронов

Будем рассматривать цилиндрический ядерный реактор, как реактор наиболее типичной для энергетических реакторов формы.

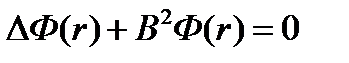
Величину геометрического параметра B будем находить из решения уравнения для критического реактора.

Пусть цилиндрический реактор имеет экстраполированные размеры: радиус R и высоту H. Здесь удобно перейти к цилиндрическим координатам. Тогда для гомогенного реактора функция потока нейтронов будет зависеть не от 3 координат (x,y,z), а от двух (r,z), так как относительно угловой координаты φ функция потока не меняется.

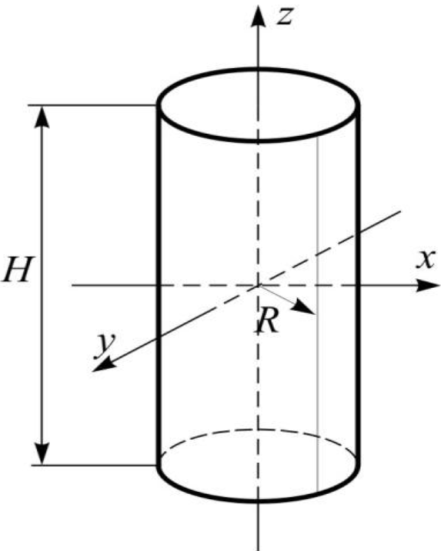
Тогда уравнение для критического цилиндрического гомогенного реактора получим в виде:

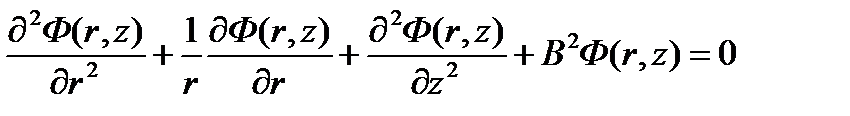(3.14)

Граничные условия: 1) 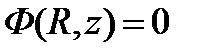, 2) 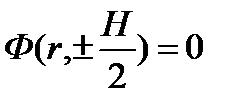. Отметим, что R и H экстраполированные размеры.

Решив уравнение (3,14), учитывая граничные условия, окончательно для пространственного распределения потока нейтронов Ф(r,z) в гомогенном цилиндрическом реакторе будем иметь:

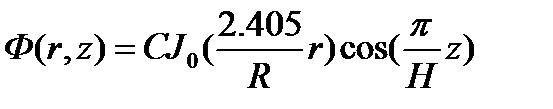(3.15)

Здесь, как и ранее, мы получили, что в критическом состоянии нейтронный поток, а, соответственно, и мощность ядерного реактора может быть любой (зависит от произвольной константы C).

Так как константа C определяет максимальное значение нейтронного потока в центре реактора, введем вместо нее константу Ф₀

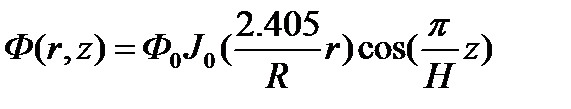(3.16)

Кроме того, можно получить выражение для геометрического параметра, как сумму радиального и аксиального геометрических параметров

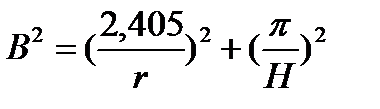, (3.17)

который из условия критичности (равенства материального и геометрического параметров) определяет критические размеры для цилиндрического гомогенного реактора без отражателя.

3.3.1. Гомогенные реакторы различной формы

По той же методике, которую мы использовали для цилиндрического реактора, можно получить функции пространственного распределения потока нейтронов и геометрические параметры для реакторов других форм:

1. Форма – бесконечная пластина

Геометрия: одномерная

Экстраполированные размеры: ширина – H

Распределение потока нейтронов: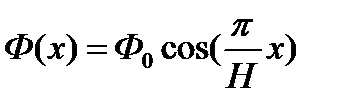

Геометрический параметр: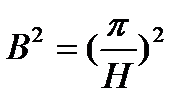

2. Форма – прямоугольный параллелепипед

Геометрия: трехмерная (декартова система координат)

Экстраполированные размеры: ширина – a; длина – b; высота – c

Распределение потока нейтронов: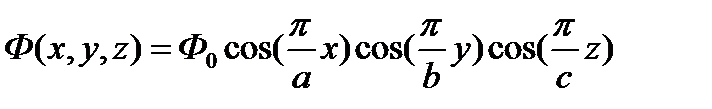

Геометрический параметр: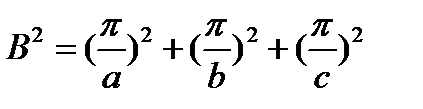

3. Форма – цилиндр

Геометрия: двухмерная (цилиндрическая система координат)

Экстраполированные размеры: радиус – R; высота – H

Распределение потока нейтронов: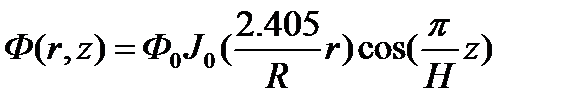

Геометрический параметр: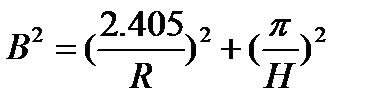

4. Форма – сфера

Геометрия: одномерная (сферическая система координат)

Экстраполированные размеры: радиус – R

Распределение потока нейтронов: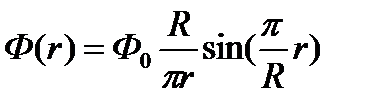

Геометрический параметр:

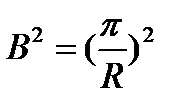
3.4. Минимальный крит. объем гомогенного голого реактора различной геометрии

Будем искать такое соотношение между радиусом и высотой цилиндрического реактора (R_onm, Н_опт), чтобы, с одной стороны, его объем был минимальным, а с другой, чтобы реактор находился в критическом состоянии.

При такой постановке задачи оптимальные радиус и высота связаны между собой, то есть при изменении, например, высоты радиус также будет изменяться. Тогда R = R(H) и условие минимальности объема реактора будет иметь вид

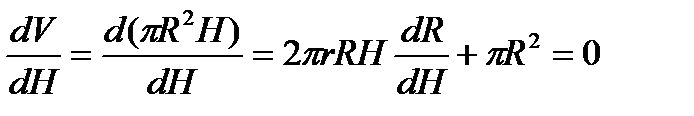(3.18)

отсюда .

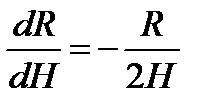С другой стороны, при оптимальных размерах реактора геометрический параметр также должен иметь экстремум. Следовательно, необходимо потребовать, чтобы

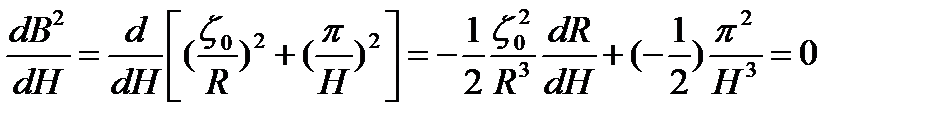(3.19)

Подставляем сюда полученное ранее соотношение для dR/dH

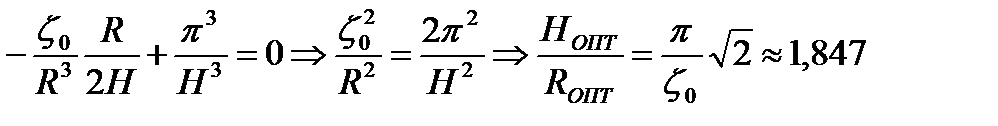(3.20)

Выразим Rопти Hоптчерез геометрический параметр B

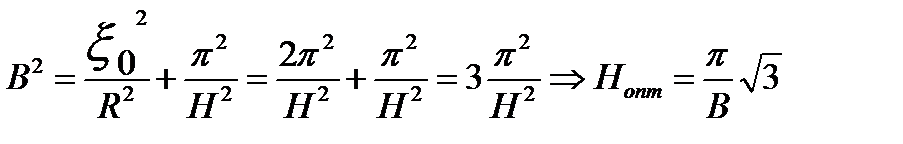
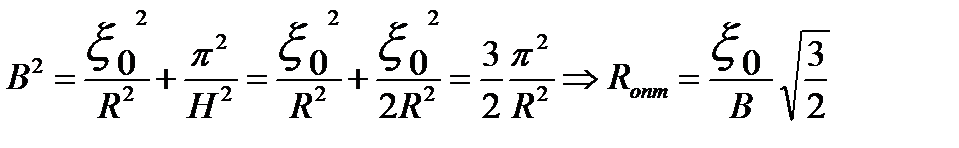
Получим значение минимального объема цилиндрического реактора

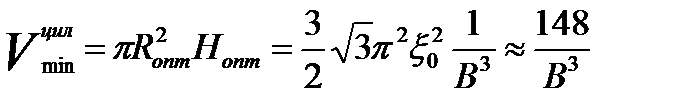(3.21)

Для реакторов других форм минимальный объем:

бесконечная пластина: не определяется

прямоугольный параллелепипед: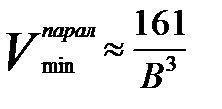

сфера: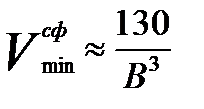

3.5. Условие критичности гомогенного реактора с отражателем в одногрупповом приближении. Эквивалентный реактор

Важным результатом, полученным нами при рассмотрении гомогенных реакторов различной формы, является наличие существенной неравномерности распределения потока нейтронов по объему реактора.

Единственной причиной неравномерности потока нейтронов в реакторе является утечка нейтронов через поверхность.

Неравномерность – это нежелательный эффект, который приводит к неэффективному использованию топлива.

В центральных областях реактора, где потоки близки к максимальным, топливо выгорает сильнее, чем на периферии. Топливо вблизи границы работает меньшей с технической недогрузкой, а значит, изменяются режимы теплоотвода, и уменьшается экономическая эффективность. Важнейшей эксплуатационной задачей в физике реакторов является обеспечение максимально возможной равномерности распределения потока нейтронов. Необходимо добиться, чтобы коэффициент неравномерности был как можно ближе к 1 (k_v →1). Основным техническим устройством, обеспечивающим выравнивание нейтронного потока, является отражатель нейтронов. Отражатель вводится добавлением на внешней поверхности реактора слоя материала, назначение которого вернуть в реактор часть нейтронов утекающих через границы.

Здесь основная идея заключается в следующем:

Родившиеся вблизи отражателя быстрые нейтроны и находящиеся на периферии тепловые нейтроны, при движении могут попадать в отражатель. В отражателе быстрые нейтроны будут эффективно замедляться и вместе с тепловыми диффундировать в его объеме. Существует ненулевая вероятность того, что тепловые нейтроны, хаотично движущиеся в отражателе, вернуться обратно в реактор. Необходимо обратить внимание, что здесь не происходит отражения от поверхности раздела «реактор – отражатель» (как, например, при оптическом отражении). Функцию возврата нейтронов выполняет весь объем отражателя - такой механизм называется диффузионным отражением тепловых нейтронов.

Будем называть ту область реактора, в которой находятся топливо, активной зоной реактора. Именно в активной зоне происходит деление ядер топлива и рождаются новые нейтроны. Гомогенная среда активной зоны является размножающей. Основная функция отражателя интенсивно замедлять быстрые нейтроны утекающие из активной зоны, создавая избыток тепловых нейтронов (по сравнению с плотностью тепловых нейтронов в активной зоне). Возникающий градиент плотности тепловых нейтронов создает нейтронный ток, направленный в сторону активной зоны, а не в сторону границы. Среда отражателя является замедляющей средой.

Соответственно нейтронно-физические свойства активной зоны и отражателя существенно отличаются друг от друга. Распределение потока нейтронов вблизи границы «активная зона – отражатель» формируется взаимными перетоками тепловых нейтронов из одной среды в другую и обратно. В пограничной с отражателем области активной формируется распределение потоков нейтронов, отличное от распределения, формируемого только за счет свойств активной зоны. Такое распределение потоков нейтронов в активной зоне носит название переходного. По мере удаления вглубь активной зоны влияние перетоков нейтронов из отражателя уменьшается, и распределение потока нейтронов будет приближаться к форме, зависящей только от параметров активной зоны. Такое распределение называют асимптотическим.

В энергетических реакторах, имеющих большие размеры, области асимптотических распределений достаточно велики. Отсюда понятно, что соотношения для реактора без отражателя являются основой для рассмотрения реактора с отражателем. Гипотетически очевидно, что при добавлении к критическому гомогенному реактору отражателя переводит его в надкритическое состояние. Соответственно, для восстановления критичности необходимо уменьшить размеры реактора. Критические размеры реактора с отражателем всегда меньше критических размеров реактора без такового. Не менее очевидно, что поскольку основная функция отражателя – замедлять нейтроны, то требования к материалу отражателя аналогичны требованиям при выборе замедлителя. Будем по-прежнему рассматривать реактор в одногрупповом приближении, то есть полагать, что все нейтроны имеют одинаковую энергию. При этом источником наших моноэнергетических нейтронов, как и ранее, являются замедлившиеся до тепловой энергии быстрые нейтроны. Реактор является гомогенным, но условие гомогенности относится независимо к двум зонам: к активной зоне (далее все, что будет касаться активной зоне будет иметь индекс «1») и к отражателю (индекс «2»).Так как две рассматриваемые области реактора разделены в пространстве, то можно записать два отдельных уравнения для каждой из них

для активной зоны:

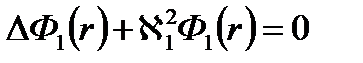
Где 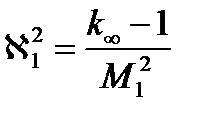– материальный параметр для среды активной зоны.

для отражателя: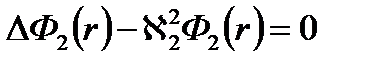

Так как среда отражателя не размножает нейтроны и здесь k_∞ = 0, материальный параметр в отражателе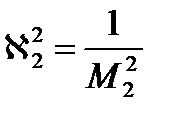

Для отражателя, состоящего чистых материалов, таких как тяжелая вода, графит, бериллий возраст нейтронов много меньше квадрата длины диффузии (τ<<L²), тогда M² ≈ L² (такая замена некорректна для легкой воды).

Записанные два уравнения связаны между собой условиями на границе раздела «активная зона –отражатель»:

1. Плотность потока нейтронов в активной зоне равна плотности потока нейтронов в отражателе на поверхности раздела сред (равенство функций).

2. Плотность диффузионного тока нейтронов в активной зоне равна плотности диффузионного тока нейтронов в отражателе на поверхности раздела сред (равенство производных).

В центре реактора (активной зоны) поток нейтронов максимальный (производные по координате, градиент равны нулю). Поток нейтронов обращается в ноль на экстраполированной границе, но теперь уже отражателя.

3.5.1. Реактор с отражателем в виде бесконечной пластины

Рассмотрим бесконечный плоский реактор, к которому с обоих сторон добавим слой отражателя. Пусть активная зона имеет толщину H, а толщины обоих боковых отражателей равны T (размер T включает длину экстраполяции). Начало координат находится в плоскости симметрии. Задача является одномерной и поток нейтронов зависит только от одной координаты x.

Тогда будем иметь уравнения следующего вида:

для активной зоны: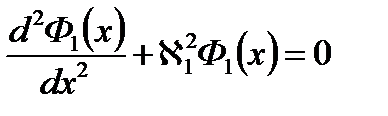

для отражателя: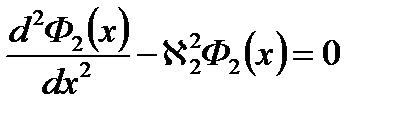

Граничные условия имеют вид

на границе раздела «активная зона – отражатель»: ,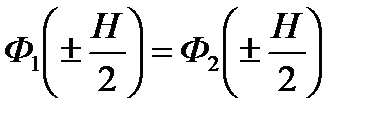

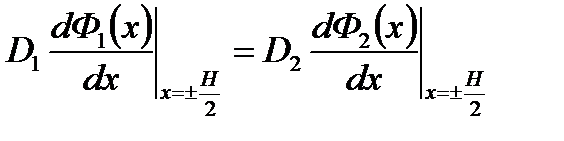
в центре активной зоны: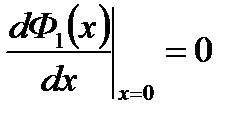

на экстраполированных границах: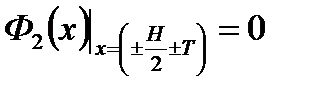

Во всех точках реактора потоки нейтронов должны быть конечны и неотрицательны.

Уравнения 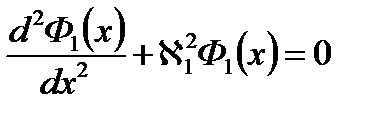и 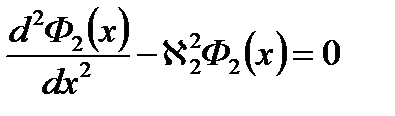являются линейными однородными уравнениями второго порядка с постоянными коэффициентами.

Корни характеристического уравнения для первого их них является мнимыми. Тогда общее решение будет иметь вид

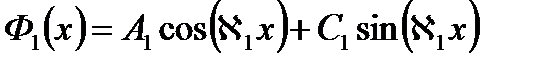
Корни характеристического уравнения для второго – является действительными и не равными друг другу. Тогда,

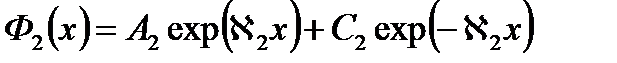
После элементарных преобразований, использования граничных условий - получим для функции потока нейтронов в отражателе:

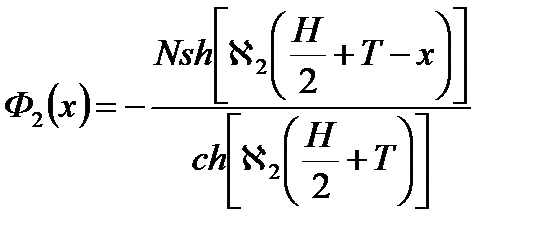или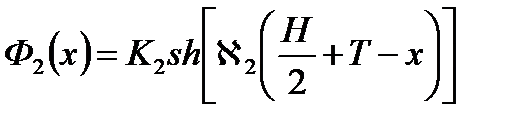

где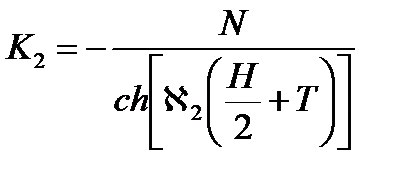

Таким образом, для плоского бесконечного реактора с отражателем будем иметь функции распределения потоков нейтронов

в активной зоне: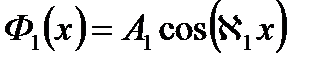

в отражателе: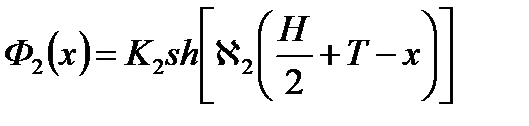

Далее необходимо установить связь между этими двумя функциями при обеспечении условий на границе «активная зона – отражатель» (x = H/2)

из равенства потоков нейтронов на границе раздела: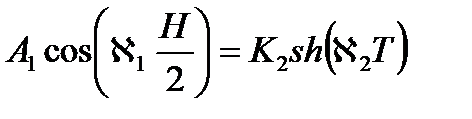

из равенства диффузионных токов: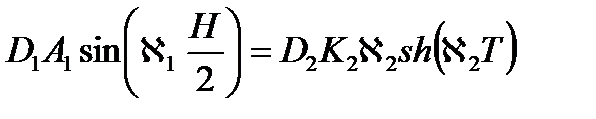

Разделим второе уравнение на первое, получим:

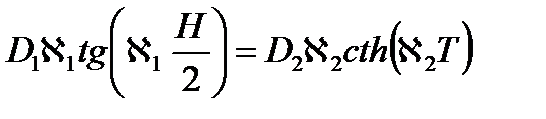
Посмотрим, что будет происходить, если мы уберем отражатель, то есть положим Т = 0.

По определению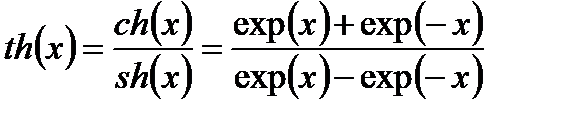

тогда при x = 0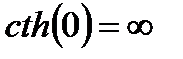

Тогда из 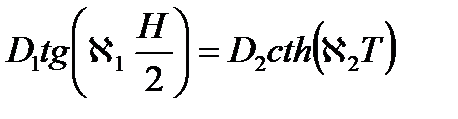следует, что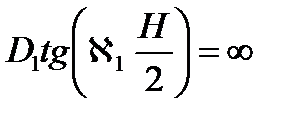

Значит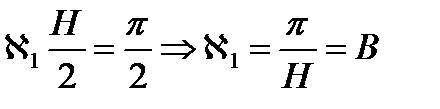

Таким образом, мы получили условие критичности реактора без отражателя.

Тогда исходное соотношение 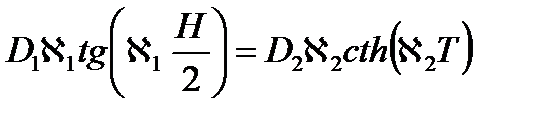является условием критичности реактора с отражателем.

Данное условие, как и в реакторе без отражателя, устанавливает связь между геометрическими параметрами (H и T) и параметрами сред, определяемыми материальным составом ( ).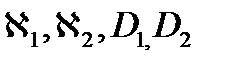

Правая часть условия критичности для реактора с отражателем зависит от функции – котангенс гиперболический.

При x=2,65 гиперболический котангенс отличается от своего асимптотического значения менее чем на 1%.

Тогда при 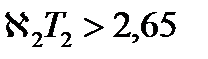толщина отражателя перестанет влиять на критические размеры активной зоны.

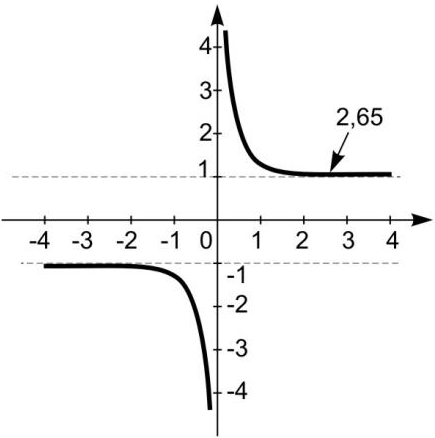
Так как и при следовательно 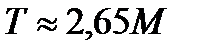тогда не имеет смысла делать отражатель больше, чем 2 - 3 длинны миграции нейтронов для материала отражателя.

3.5.2. Эффективные размеры активной зоны для
реактора с отражателем. Эквивалентный реактор.

Будем называть размеры активной зоны реактора, увеличенные на величину эффективной добавки за счет отражателя, эффективным размером активной зоны.

Например, для реактора в форме бесконечной пластины эффективный размер определится как:

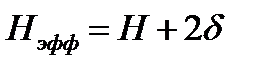
δ – эффективная добавка за счет отражателя.

Для цилиндрического реактора, окруженного со всех сторон отражателем:

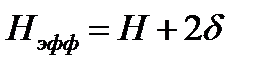и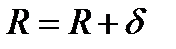

При размерах активной зоны, равных эффективному размеру, такой гипотетический реактор будет находиться в критическом состоянии.

Тогда при проведении анализа на критичность можно воспользоваться моделью – эквивалентным реактором.

Эквивалентный реактор – это реактор без отражателя, в котором влияние отражателя на поток нейтронов заменено увеличенным размером.

Соответственно, для эквивалентного реактора будет выполняться условие критичности для реактора без отражателя, то материальный параметр будет равен геометрическому.

Например, для цилиндрического реактора:

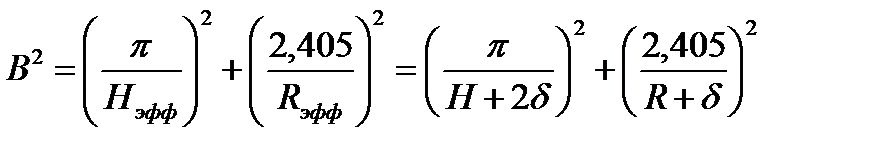
Очевидно, что в этом случае эффективный коэффициент размножения определится соотношением: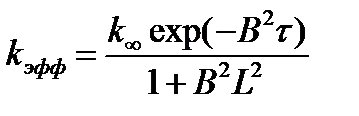

Таким образом, использование модели эквивалентного реактора позволяет для реактора с отражателем применить более простые соотношения, что существенно упрощает проведение оценочных расчетов.

Так как эквивалентный реактор – это реактор без отражателя, то потоки нейтронов на его границе обращаются в ноль.

Тогда становится понятен физический смысл эффективной добавки за счет отражателя.

Эффективная добавка за счет отражателя – это расстояние, отсчитываемое от границы активной зоны, на котором асимптотическое распределение потока нейтронов обращается в ноль.

3.6. Условие критичности гомогенного реактора с отражателем в двухгрупповом приближении. Распределение тепловых нейтронов в отражателе

Решение уравнения диффузии для ЯР с отражателем в одногрупповом приближении приводит к значительным погрешностям.

Проведенная выше оценка эффективной добавки отражателя δаз занижена по двум причинам:

- быстрые нейтроны, попавшие в отражатель, имеют большую вероятность возвратиться в а.з. в результате столкновений в отражателе;

- нейтроны, попавшие в отражатель при энергии большей, чем резонансная энергия поглощения в а.з., могут вернуться в а.з. с энергией ниже резонансной.

Пусть все нейтроны делятся на две группы: первая – быстрые (1 – БН) и вторая – тепловые (2 – ТН).

Для каждой̆ группы в а.з. и в отражателе записывается уравнение диффузии в одной из форм, рассмотренных ранее в курсе «Теория переноса нейтронов». Для а.з. ЯР:

, (*)

; (**)

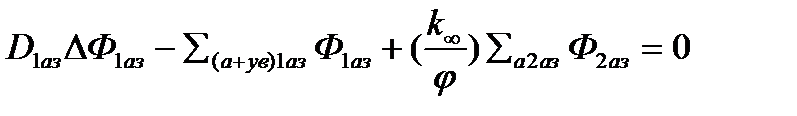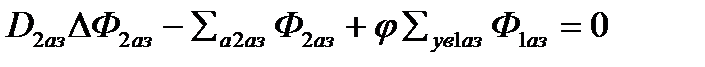Для отражателя (k_∞=0, делящихся ядер нет и вероятность избежать резонансного радиационного захвата φ=1):

,(***)

, (****)

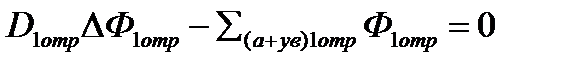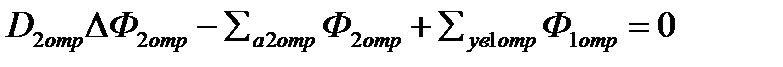где ∑_{(a+ув)1аз}=∑_a1аз+∑_ув1аз – суммарное сечение поглощения + увода нейтрона из первой группы (БН поглощается или становится ТН, обычно ∑_a1аз<<∑_ув1аз и ∑_{(a+ув)1аз}≈∑_ув1аз);

(k_∞/φ)∑_a2азФ_2аз – источник нейтронов в первой группе за счет поглощения нейтроноввторой группы (ТН);

φ∑_ув1азФ_1аз – источник нейтронов во второй группе – приход нейтронов из первой группы в силу увода БН.

Предполагается, что поглощение БН происходит на границе двух групп при некоторой энергии Е=Е_гр, при этом поток нейтронов скачком убывает в φ раз, где φ – вероятность для нейтрона избежать резонансного радиационного захвата в уране-238.

В приведенных уравнениях для а.з. для БН как источник учитываются ТН, а для ТН как источник учитываются БН, т.е. уравнения для а.з. симметричны относительно потоков. Это позволяет предположить, что потоки БН и ТН описываются волновыми уравнениями с одним и тем же собственным числом χ²_аз:

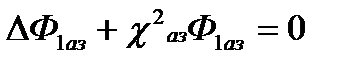, (1)

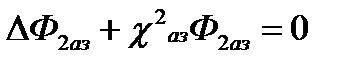, (2)

Подставляя в предыдущее уравнение

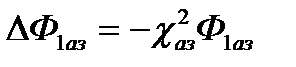и 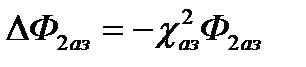, имеем для а.з.

,

.

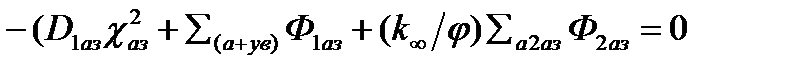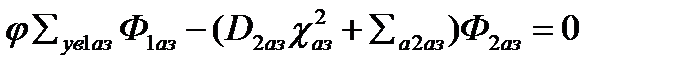Решение данной системы нетривиально при равенстве нулю ее определителя:

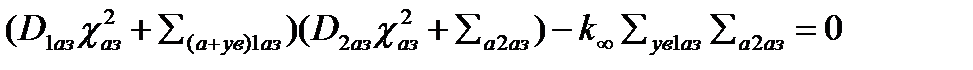
или

,

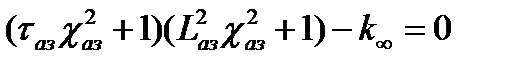где , .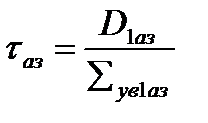

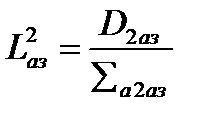Тогда 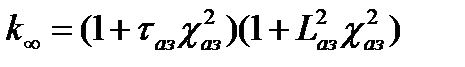, где χаз2 – искомая величина. Данное биквадратное уравнение имеет два решения относительно χаз2: χ1аз2 и –χ2аз2, которым соответствуют свои квазистационарные решения уравнения диффузии.

3.7. Коэффициенты неравномерности поля энерговыделения в ядерных реакторах. Способы выравнивания поля энерговыделения

В случае профилирования ядерного топлива, как это имеет место в реакторах ВВЭР, вместо коэффициентов неравномерности распределения плотности потока нейтронов используются коэффициенты неравномерности тепловыделения, определяющие степень отклонения энерговыделения в различных точках активной зоны от среднего значения.

Коэффициенты неравномерности тепловыделения определяются как отношения максимальных значений удельного объемного тепловыделения по координатам к его средним значениям по соответствующим координатам.

Максимальный коэффициент неравномерности по объему определяет допустимую мощность ядерного реактора:

,

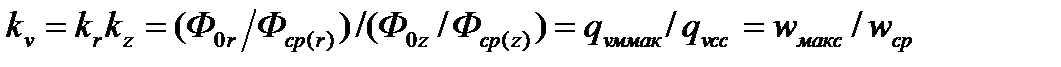где:

- w_макс, w_ср - максимально допустимая и средняя удельная мощность в активной зоне;

-k_r, k_z - максимальные коэффициенты неравномерности тепловыделения по радиусу и высоте активной зоны.

Коэффициент неравномерности по радиусу активной зоны (k_R) - число, показывающее, во сколько раз максимальная по радиусу активной зоны величина плотности потока тепловых нейтронов больше среднерадиального её значения:

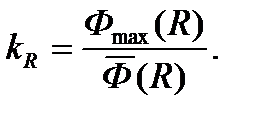(9.5.1)

Если известна функция распределения по радиусу активной зоны Ф(R), то среднерадиальное её значение найдется как:

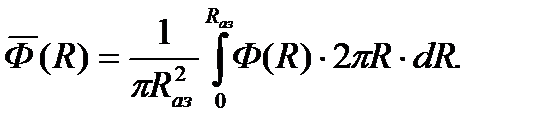(9.5.2)

В этом случае общее выражение для k_R:

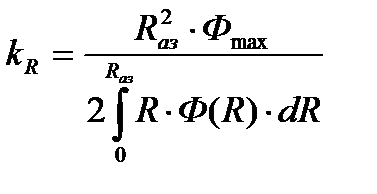9.5.3

Если оценить величину k_R в гомогенной цилиндрической активной зоне, где радиальное распределение плотности потока тепловых нейтронов подчинено закону:

Ф(R) = Ф_max I_o[2.405R/(R_аз+d_э)] (9.5.4)

То подстановка этого выражения в (9.5.3), взятие интеграла и простое математическое преобразование полученного выражения с учётом того, что величина эффективной добавки d_э пренебрежимо мала по сравнению с величиной радиуса активной зоны R_аз, приводят к приближённой формуле:

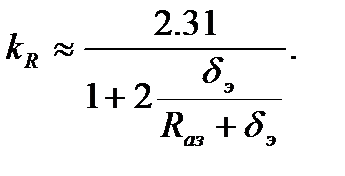(9.5.5)

Следовательно, если бы такой реактор, как ВВЭР-1000 был гомогенным реактором (R_аз = 156 см, d_э » 10 см), ему был бы обеспечен коэффициент радиальной неравномерности:

k_R » 2.31 / [1 + 2 ^.10/(156 + 10)] » 2.062.

Коэффициент нерав