Одногрупповое диффузионное приближение.

Распространение нейтронов в среде можно рассматривать аналогично

процессу диффузии газа в атмосфере и применять закон Фика и уравнение

диффузии.

Диффузионное приближение справедливо только при следующих условиях:

- нейтрон рассматривается как точечная частица и пренебрегается нейтрон-нейтронным взаимодействием, считается, что энергия тепловых нейтронов практически не меняется при столкновениях с ядрами среды;

- ядра среды должны быть достаточно тяжелыми для обеспечения

изотропного рассеяния (для поправки на анизотропность рассеяния вводят

транспортные величины);

- макроскопические сечения рассеяния должны быть неизменными

или, в крайнем случае, слабо зависеть от пространственных координат;

- среда не должна содержать сильно локализованных источников или

поглотителей нейтронов, поток нейтронов должен слабо меняться на длине

свободного пробега нейтрона, что часто выражается условием λ∇ф/ф<< 1

При решении уравнения диффузии всегда рассматривается «средний» нейтрон. Рождающиеся в реакциях деления свободные нейтроны двигаются хаотично, рассеиваясь на ядрах среды на произвольные углы и замедляясь. При этом расстояние между столкновениями, угол рассеяния, скорость, энергия являются случайными величинами, т.е. не являются постоянными и не могут быть выражены функцией от времени. Для того чтобы решить уравнение диффузии с коэффициентами, зависящими от этих случайных величин, вводят понятие нейтрона с усредненными параметрами. Такой нейтрон всегда имеет одну и ту же скорость между столкновениями (хотя реально скорость может и расти, и уменьшаться), проходит одно и то же расстояние между двумя последовательными столкновениями, одно и то же число столкновений в единицу времени, а также всегда имеет одинаковый угол рассеяния π/2 .

Плотность потока нейтронов Ф можно определить как число нейтронов ΔN пересекающих в единицу времени Δt единицу площади ΔS.

Ф = ΔN/(Δt* ΔS) [см^-2*с^-1] или [нейтр./см²*с]

Всегда имеет место направленное перемещение нейтронов из области с большей плотностью потока нейтронов Ф в область с меньшей плотностью потока нейтронов Ф. Это смещение описывается, векторной величиной называемое током нейтронов.

Результирующий ток нейтронов описывается законом Фика:

J = -D*gradn ,гдеD – коэффициент диффузии.

Баланс нейтронов в единице объема определяется тремя процессами

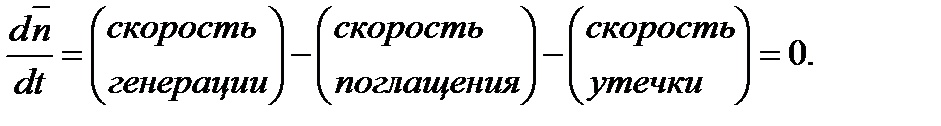(4.1.1)

Скорость генерации нейтронов [нейтр./см³с] – число нейтронов, появляющихся(рождаемых) в единицу времени в единичном объеме 1 см³

– можно записать как функцию S(r,t).

Скорость поглощения [нейтр./см³с] – число нейтронов, поглощаемых в единицу времени в единичном объеме 1 см³среды – можно записать в

виде ∑a(r)Ф(r,t)

Скорость утечки описывается выражением P(x,y,z)= -DΔ Ф(x,y,z) (4.1.2)

Или

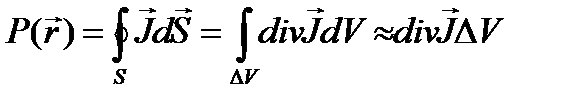(4.1.3)

Подставляя в условие баланса нейтронов выражения для скоростей генерации поглощения и утечки нейтронов, получим уравнение диффузии нейтронов для среды, свойства которой изменяются плавно

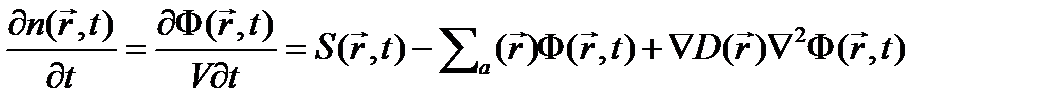(4.1.4)

При скачкообразном (резком) изменении свойств, например, на границах сред, необходимо для каждой среды записывать это уравнение с соответствующими граничными условиями. Для однородной среды, свойства которой не зависят от координат

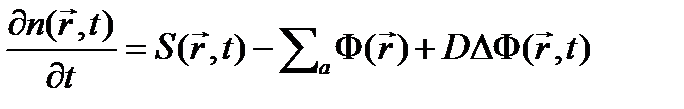(4.1.5)

Уравнение диффузии для стационарной задачи (нет переменной времени)

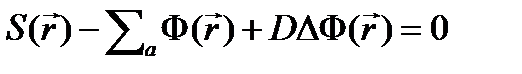(4.1.6)

Граничные и прочие условия для нахождения решения уравнения диффузии для элементарных геометрий:

1) Условие на выпуклой границе среды с вакуумом для конечных или

полубесконечных сред;

2) условия на границе раздела сред с различными физическими

свойствами;

3) условие в окрестности внешних локализованных источников;

4) условие ограниченности и неотрицательности нейтронного потока;

5) начальные условия в нестационарных задачах (где есть зависимость

от времени по переменной t)

1) Условие на выпуклой границе среды с вакуумом для конечных или

полубесконечных сред.

Диффузионное приближение плохо описывает распределение плотности потока нейтронов в окрестностях границы среды с вакуумом, так как на границе резко меняются свойства сред. Строгая формулировка граничных условий в этом случае возможно лишь при решении газокинетического уравнения Больцмана методами теории переноса. В рамках диффузионного приближения можно задать граничные условия, при которых решение уравнения диффузии не будет приводить к существенным отклонениям от действительности.

Выпуклой называют такую границу среды с вакуумом (рис. 1, а), пересечение которой нейтроном по всем направлениям не приводит к возврату нейтрона обратно в среду при условии, что он движется все время

прямолинейно.

Рис. 1. Выпуклая (а) и невыпуклая граница (б)

Это можно сформулировать так: нейтрон, вылетевший в вакуум обратно не возвращается (воздух для нейтронов также считается вакуумом).

В связи с этим, односторонний ток нейтронов из вакуума в среду равен нулю. Обозначая через r₀ вектор, определяющий положение пространственных точек выпуклой границы среды с вакуумом, можно записать в общем случае:

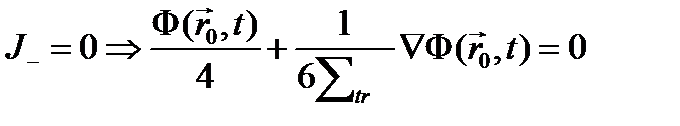(4.1.7)

Это условие справедливо для «голого» реактора – реактора без отражателя.

С учетом длины линейной экстраполяции δ =2λ_tr/3 = 2/3Σ_tr эту функция можно записать в виде:

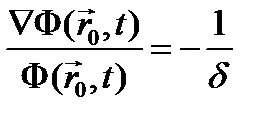(4.1.8)

Из решения газокинетического уравнения Больцмана для сред слабо

поглощающих нейтроны следует, что δ = r_э–r₀=0,71λ_tr.

Убывающую функцию в случае скачкообразного изменения в какой-

либо точке можно экстраполировать к нулю непрерывным образом. В пограничном слое в силу утечки части нейтронов в вакуум (пустота и воздух не отражают нейтроны) уже на расстоянии, равном транспортной длине, происходит нарушение изотропии диффузии. Применять уравнение диффузии в малой приграничной области нельзя. Точный переход диффузионного потока в направленный поток за пределами тела (активной зоны – а.з.) дает только решение кинетического уравнения Больцмана. Поэтому распределение плотности потока нейтронов из тех внутренних областей, где справедлива теория диффузии, экстраполируется за пределы тела r₀ линейно.

Рассмотрим одномерный случай или случай сферической симметрии.

Зададим линейную (экстраполируем линейно) зависимость плотности потока нейтронов на границе среды с вакуумом в вакуум (рис. 2)

Ф(r) = Const₁r + Const₂ (4.1.9)

Точка, в которой происходит обращение экстраполированного потока в нуль, принимается за условную границу тела (а.з.) r_э, тогда

Ф(r_э) = Const₁r_э + Const₂ =0 (4.1.10)

Откуда r_э= -Const₂/Const₁ (4.1.11)

Из ф. (4.1.8), получаем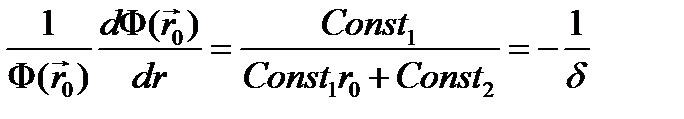

Откуда Const₂/ Const₁ = -( δ+ r₀).

Сучетом ф. (4.1.11) Const₂/Const₁ = -( δ+ r₀) = r_э

Окончательно имеем, что δ = r_э–r₀ (4.1.12)

Отсюда становится ясен смысл параметра δ . Это расстояние от реальной границы тела (среды), на котором происходит обращение экстраполированного потока нейтронов в нуль

Ф(r,t)=0 (4.1.13)

Ф. (4.13) называют условием для плотности потока нейтронов на экстраполированной границе среды с вакуумом.

Рис. 2. Экстраполированная граница:δ = r_э–r₀

2) Условия на границе раздела сред с различными физическими

свойствами.

Если рассматриваемая а.з. (тело) состоит из нескольких сред, то для простоты считают, что свойства сред не зависят от координат внутри этих сред, а изменяются лишь на их границах – макросечения реакций в данном случае являются кусочно-постоянными функциями координат, терпящими разрыв на границе сред r₀. Количество нейтронов, вылетающих в единицу времени из одной среды должно равняться количеству нейтронов, влетающих в единицу времени в другую среду, и наоборот (равенство односторонних токов). Условия сшивки решений имеют вид:

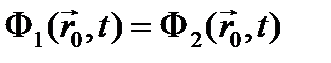(4.1.14)

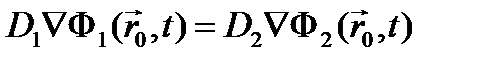(4.1.15)

где D_i (i=1,2) – коэффициенты диффузии соответствующих сред.

По сути, ф. (4.1.14), ф. (4.1.15) – требования непрерывности плотности потока нейтронов и проекций на нормаль к границе раздела плотности тока нейтронов при переходе границы раздела сред.

3) Условие локализованных источников.

Пусть в не размножающей нейтроны среде в точке r₀ расположенточечный источник моноэнергетических нейтронов с постоянной вовремени (стационарной) мощностью S. Нейтронное поле, создаваемоеэтим источником, также будет стационарным – не зависящим от времени.

Выделим в окрестности источника сферу радиуса R площадью поверхности S_R и объемом V_R. Если в уравнении диффузии вида (4.1.6) представить скорость утечки в единице объема в виде ф. (4.1.3) P( r)= divJΔVи применить теорему Остроградского–Гаусса ∫divJdV = ∫JdS (!) ,а затем перейти к пределу при R →0 , то получим

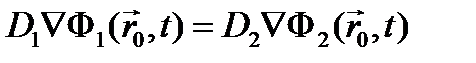
Тогда условие локализованного источника имеет вид

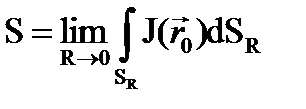(4.1.16)

Это условие следует понимать как равенство числа испускаемых источником в единицу времени нейтронов числу нейтронов, утекающих сквозь поверхность элементарной сферы с источником в центре при ее радиусе, стремящемся к нулю.

4) Условие ограниченности и неотрицательности нейтронного потока.

Согласно физическому смыслу нейтронный поток не может быть бесконечно большим и отрицательным, т.е.

0 ≤Ф(r,t)< ∞ (4.1.17)

5) Начальные условия в нестационарных задачах.

Для решения нестационарного уравнения, необходимо знать распределение плотности потока нейтронов в момент времени t=0

f(r)=Ф( r,0) (4.1.18)

Решение уравнения диффузии в средах.

1. Бесконечная однородная среда.

Найдем поле моноэнергетических нейтронов, генерируемых в бесконечной однородной среде точечным изотропным источником с постоянной во времени скоростью генерации S_T, нейтр/с, расположенным в начале координат. Уравнение диффузии во всем объеме среды, кроме точки r=0, есть

DΔФ(r) - ∑_aФ(r)=0 (4.1.19)

Ввиду сферической симметрии задачи и однородности среды уравнение (4.19) удобно записать в форме

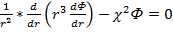(4.1.20)

где χ²=∑_а/D (4.1.21)- параметр, определяющий свойства среды.

Условия задачи сформулируем следующим образом

1) поток нейронов ограничен;

2) полное число нейтронов, поглощаемых в единицу времени, равно скорости их генерации (условие баланса для стационарной задачи) , т.е.

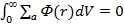(4.1.22)

Для упрощения формы уравнения (4.1.20) сделаем подстановку Ф=u/r и приведем его к виду d²u/dr² – χ²u = 0 (4.1.23)

Общее решение уравнения (4.23) есть

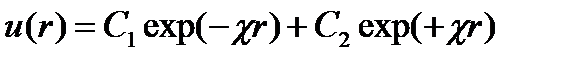(4.1.24)

Соответственно для Ф(r)

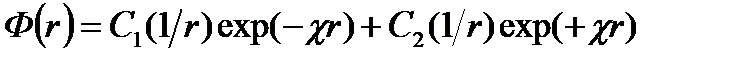(4.1.25)

Из условия 1 следует, что С₂=0. Тогда

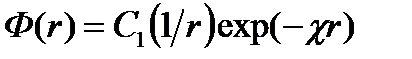(4.1.26)

Для определения константы С₁ воспользуемся вторым условием (4.1.22). Подставляя в него выражение для потока(4.1.26), имеем

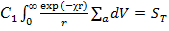(4.1.27)

Вычисляя интеграл, получаем С₁ = S_T/(4πD) и

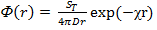(4.1.28)

В природе не существует точечных источников конечного размера. Поэтому полученное решение при r=0 не имеет физического смысла. По формуле (4.28) можно рассчитать распределение потока нейтронов во всем пространстве, кроме точки r=0 , в которой размещен источник. Однако, что вблизи источника диффузионное приближение не дает правильного результата, так как не выполняется условие (4.1.22). Сравнение с точным решением показывает, что хотя поток нейтронов и стремится к бесконечности при r→0, все же диффузионное приближение значительно занижает его значение в окрестности источника.

Полученное выражение для потока нейтронов (4.1.28) можно представить в более общем вид, если источник нейтронов расположен не в начале координат, а в любой точке пространства r’:

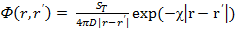(4.1.29)

Функция 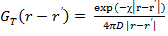(4.1.30) называется диффузионной функцией влияния точечного источника. Она имеет следующий физический смысл: это поток нейтронов в точке r, обусловленный наличием в точке r точечного источника, испускающего 1 нейтрон за 1с. Выражение (4.1.30) иногда называют также «точечным» диффузионным ядром.

2. Конечная однородная среда.

В качестве примера рассмотрим случай, когда точечный источник со скоростью генерации S_T расположен в центре сфере радиусом R. Совместим начало координат с центром сферы и найдем распределение потока нейтронов, воспользовавшись полученным ранее общим решением (4.1.25).

Для определения одной из постоянных имеем условие обращения потока нейтронов в нуль на экстраполированном радиусе сферы R_э:

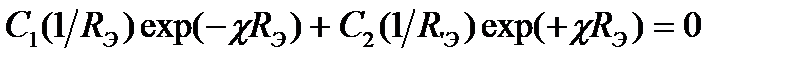
Отсюда

С₂ = С₁exp(-2χR_э) и 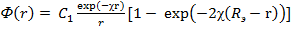(4.1.31)

Чтобы найти С₁, воспользуемся условием

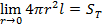
Смысл этого условия очевиден – ток нейтронов через сферу, как угодно близко охватывающую источник, равен скорости генерации этого источника. Поскольку 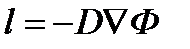, то дифференцируя выражение (4.1.31) по r и устремляя r→0, находим .

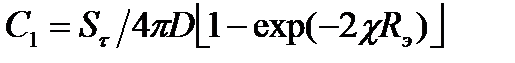Окончательно

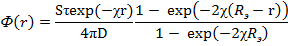
Отличие от полученного ранее выражения для потока нейтронов в бесконечном пространстве (4.28) учитывается вторым сомножителем. Этот сомножитель способствует ускорению спада потока нейтронов в конечном объеме по сравнению с бесконечным.

Одногрупповые константы.

Строго говоря, функция плотности потока нейтронов зависит не только от пространственных координат, но и от энергии нейтронов - Ф(r, Е).

В общей физике показывается, что поведение отдельного, не взаимодействующего с другими частицами, атома в каждый момент времени можно полностью описать 6 координатами (6-мерное пространство): 3 пространственные координаты x,y,z и 3 составляющие импульса p_x,p_y,p_z.

Для коллектива невзаимодействующих нейтронов состояние нейтрона описывается 5 переменными – тремя пространственными координатами (x,y,z или r) , энергией нейтрона Е, временем t.

Рассмотрим стационарное пространственно-энергетическое распределение нейтронного поля. Для этого запишем уравнение баланса скоростей всех процессов, протекающих в элементарном объеме фазового пространства dVdE, где dV –элементарный объем в окрестности точки r, а dE – элементарный интервал энергий в окрестности значения энергии Е.

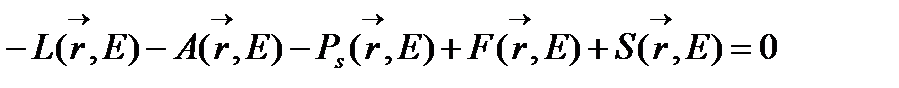
или

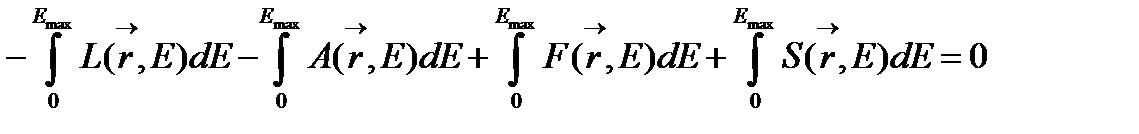
Где, первое слагаемое - L(r, E) – количества нейтронов, покидающих в единицу времени рассматриваемый фазовый объем dVdE за счет пространственной миграции;

Второе - А(r , E) – количество нейтронов, поглощаемых в единицу времени в рассматриваемом фазовом объеме dVdE;

Третье слагаемое - P_s(r,E) - количества нейтронов,покидающих в единицу времени рассматриваемый фазовый объем dVdE за счет рассеяния на ядрах среды;

Четвертое слагаемое R_s(r,E) – количество нейтронов, появляющихся в единицу времени рассматриваемом фазовом объеме dVdE за счет рассеяния на ядрах среды, т.к. рассматривается стационарный случай, то ;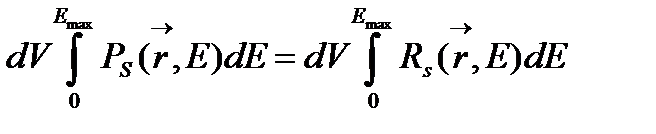

Пятое слагаемое - F(r,E) – количество нейтронов, генерируемых в единицу времени в рассматриваемом фазовом объеме dVdE за счет деления ядер среды;

Шестое слагаемое - S(r,E) –количество нейтронов, генерируемых в единицу времени в рассматриваемом фазовом объеме dVdE внешними для данного элемента объема dV источниками нейтронов.

Так как коэффициенты уравнения диффузии являются функциями многих переменных, для упрощения решения задачи их усредняют по всему энергетическому спектру нейтронов. В одногрупповом приближении усредненные по всему спектру энергии нейтронов величины определяются:

плотность потока нейтронов 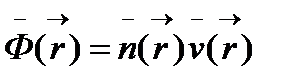(4.1.38)

плотность нейтронов 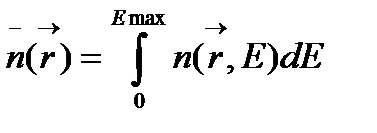(4.1.39)

скорость нейтронов 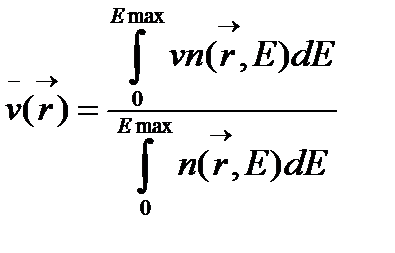(4.1.40)

макросечение поглощения 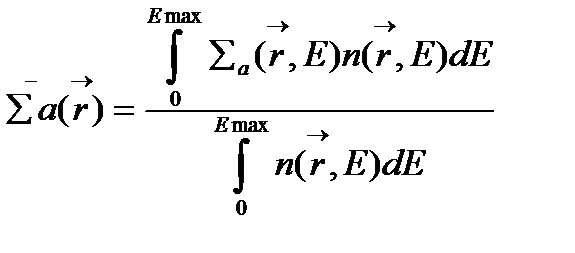(4.1.41)

транспортное макросечение 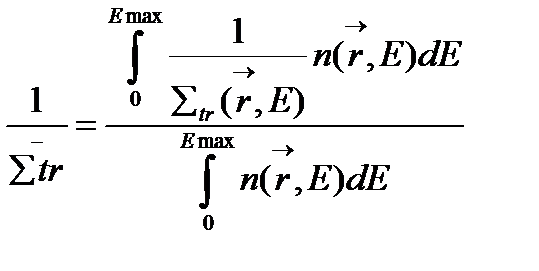(4.1.42)

коэффициент диффузии 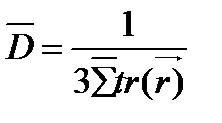(4.40)

параметр деления 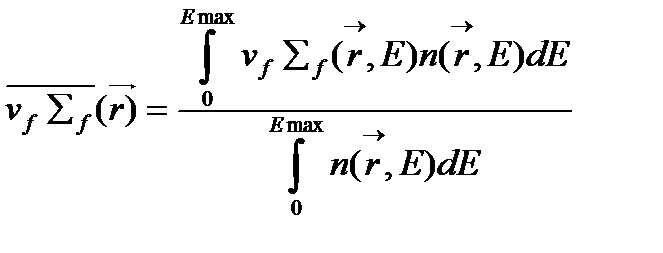(4.1.43)

мощность источника 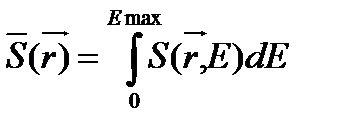(4.1.44)

В силу сложности задачи пусть в каждой точке среды нейтронное поле имеет распределение (спектр нейтронов) f(Е), т.е.

n(r, E) = n(r)f(E) (4.1.45)

при этом для функции f(Е) выполняется условие нормировки

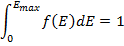
Усреднение характеристик полиэнергетического коллектива нейтронов, в идеале, необходимо проводить по всему спектру конкретного ЯР, но это всегда искомая величина. Поэтому, в первом приближении, усреднение всех параметров проводят по известным спектрам Уатта (для БН), Ферми (для замедляющихся нейтронов), Максвелла (для ТН), функции распределения которых известны.

4.2. Многогрупповое уравнение для плотности потока нейтронов и его решение.

Для решения задач физики ядерных реакторов мы использовали одногрупповой метод. Мы полагали, что в реакторе присутствуют нейтроны только одной энергии, то есть эти нейтроны являются тепловыми. В качестве источника тепловых нейтронов мы рассматривали нейтроны, которые замедлились до тепловой энергии, избежав резонансное поглощение и утечку. Такой подход позволил нам получить ряд фундаментальных результатов физики реакторов, которые составляют ее основу. В том числе мы исследовали влияние отражателя на распределение нейтронного потока и на критичность реакторов различной формы. До настоящего времени мы считали, что нейтроны с энергиями, отличными от тепловой не оказывают влияния на работу реактора и служат лишь источником тепловых нейтронов.

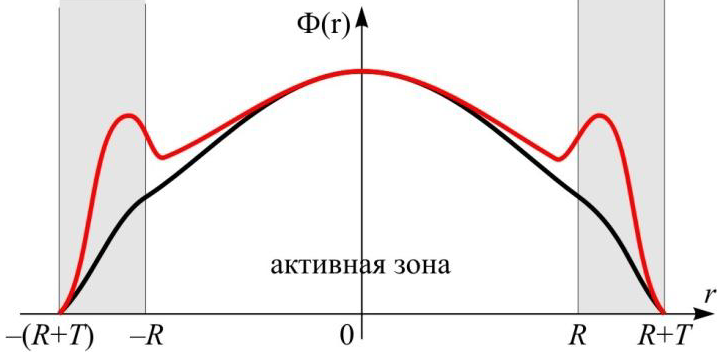
Очевидно, что такое приближение с большим количеством допущений является самым первым, оценочным приближением. Оно пригодно для гомогенных реакторов больших размеров. С уменьшением размеров активной зоны точность результатов значительно падает. При рассмотрении гомогенного реактора с отражателем мы получили ряд результатов, которые можно рассматривать как интегральные и качественные.

Дифференциальное по пространству распределение нейтронного потока в реакторе с отражателем в одногрупповом приближении далеко от ситуации близкой к реальной картине.