Функция ценности нейтронов.
Средняя энергия ЗН составляет 0,49 МэВ. Это примерно в 4 раза меньше средней энергии МГН (около 2 Мэв).
Отсюда следует, что вероятность избежать утечки в процессе замедления для ЗН выше, чем для МГН. Значит, ЗН обладают более высокой потенциальной возможностью к дальнейшему размножению, чем МГН. Это свойство запаздывающих нейтронов характеризуется так называемой ценностью ЗН.
Различие ценности ЗН и МГН учитывается фиктивным увеличением доли ЗН, т.е. считается, что ЗН имеют такую же среднюю энергию, как и МГН, но их эффективная доля bэф превышает фактическуюb.
Это увеличение доли ЗН осуществляется посредством умножения b на ценность запаздывающих нейтронов g:
bэф= bg.
Ценность запаздывающих нейтронов g для различных реакторов:
| ЯР | Диаметр а.з. мм | Высота а.з. мм | Ценность ЗН g |
| Учебный реактор ИР - 100 | 1,25 | ||
| Транспортный реактор ОК - 350 | 1,08 | ||
| Реактор ВВЭР - 1000 | 1,008 | ||
| Реактор РБМК - 1000 | 1,0005 |
Для ВВЭРg= 1+ 20b2@ 1,05 ÷1,1.
Нейтроны, введенные вблизи внешней границы, вызовут меньшее увеличение потока нейтронов, чем нейтроны, введенные вблизи центра ЯР. Следовательно, поток нейтронов возрастет на некоторую величину, причем не только в точке r, а по всему ЯР.
Если проинтегрировать возникшее изменение потока нейтронов по объему ЯР, то полученное значение будет равно числу введенных нейтронов, умноженную на вероятность избежать утечки.
На величину изменения потока нейтронов будет также влиять энергия введенных нейтронов.
Таким образом, с точки зрения внесенного в ЯР возмущения нейтроны имеют различную ценность, которая зависит от энергии и координаты.
Определим функцию ценности нейтронов, как величину, пропорциональную величине потока (распределенного по энергии и пространству), возникающего при введении в реактор одного нейтрона.
Введем понятие статистического веса нейтрона, как произведение потока и ценности нейтронов для получения более качественной малогрупповой системы уравнений.
Статистический вес будет нужен нам для более корректной свертки смежных групп в одну широкую группу.
При этом однако оператор, связанный с уравнением переноса, не является самосопряженным, т.е. не удовлетворяет условию для функций
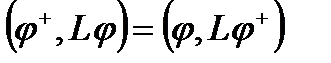
Если оператор Lнесамосопряженный, то сопряженный ему оператор L+, действующий на функцию φ+ можно определить из условия
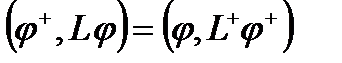
Функцию φ+ называют сопряженной функцией.
Сопряженная функция для функции потока нейтронов есть функция ценности нейтронов, которую далее будем обозначать Ф+.
С учетом оператора L=DΔ-Σa+νΣf
DΔФ-ΣaФ+νΣfФ=0 или LФ=0
В точке r оператор Лапласа после воздействия на функцию потока дает действительное число. Все остальные слагаемые оператора L также действительные числа. В этом случае сопряженный оператор L+ совпадает с оператором L.
Следовательно, для функций ценностей нейтронов получим уравнение вида
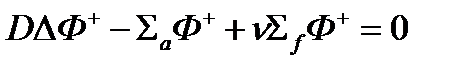
Это уравнение ничем не отличается от уравнения для потоков нейтронов, следовательно, функции потоков и ценностей нейтронов в ЯР без отражателя в одногрупповом приближении в точности совпадают 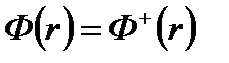
Дата добавления: 2021-05-28; просмотров: 831;











