Решение многогруппового уравнения для эквивалентного реактора

Запишем многогрупповое уравнение в следующем виде

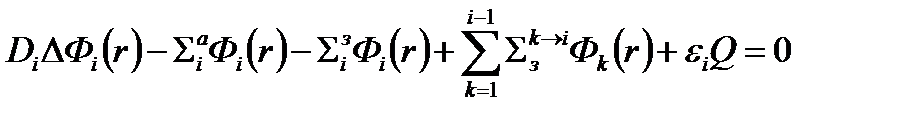(4.2.21)
Где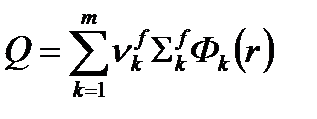

Рассмотрим критический эквивалентный реактор, для которого в каждой группе справедливо уравнение 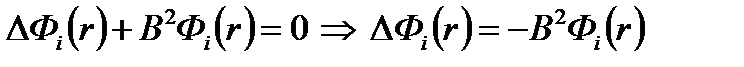(4.2.22)

Подставим последнее выражение в многогрупповое уравнение и проинтегрируем его по всему объему реактора, то есть перейдем от дифференциального распределения потока нейтронов по координате к интегральным потокам: Ф_i(r)→Ф_i

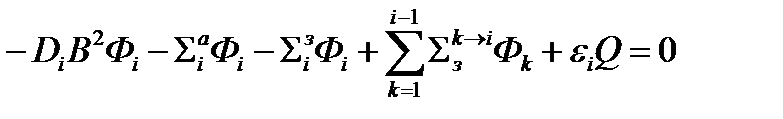(4.2.23)

Выразим от сюда Ф_i

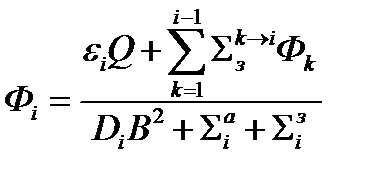
Вместо системы многогрупповых дифференциальных уравнений получили систему алгебраических уравнений, из которой может быть найден интегральный по объему спектр нейтронов.

Решение полученной системы может быть получено итерационным методом.

1) Полагаем в первой итерации Q⁽¹⁾ = 1 н*см^–2с^–1, найдем плотности потоков нейтронов для каждой группы

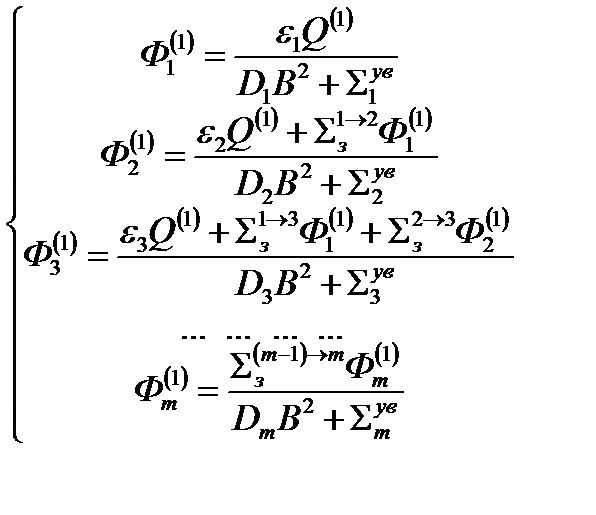
2) Полученные потоки нейтронов Ф⁽¹⁾_i используем для вычисления полного числа нейтронов деления на новой итерации

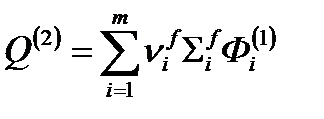
3) Используем рассчитанное значение для источника нейтронов на новой итерации для определения новой последовательности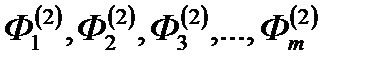

4) По полученному энергетическому распределению потоков нейтронов Ф⁽²⁾_i вычисляем полное число нейтронов деления на следующей итерации Q⁽³⁾

5) На каждой итерации рассчитываем отношение Q⁽ⁿ⁺¹⁾/Q⁽ⁿ⁾

6) Очевидно, что итерационный процесс следует прекратить, когда отношение, рассчитанное в п.5 перестанет изменяться в рамках заданной точности.

Если рассматривать нейтроны деления полученное на (n+1)-ойитерации, как новое поколение нейтронов, а нейтроны деления на n-ой итерации, как нейтроны предыдущего поколения, тогда отношение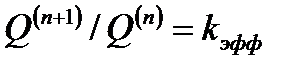

Полученная на последней итерации последовательность 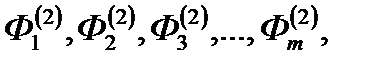является искомым спектром интегральных потоков нейтронов.

Найденный эффективный коэффициент размножения должен соответствовать параметрам рассчитываемого реактора.

Если последнее условие не выполняется, то конструкция реактора должна быть изменена и вычисления выполнены заново.

По найденному спектру нейтронов может быть получено пространственное распределение потоков нейтронов.

Очевидно, что пространственное распределение в эквивалентном реакторе зависит от его геометрической формы и определяется условиями равенства нулю потоков нейтронов всех групп на внешней экстраполированной границе.

Длинна экстраполяции зависит от транспортной длинны пробега нейтронов, которая в свою очередь зависит от энергии. Следовательно, для каждой группы нейтронов свое значение экстраполированного размера.

Например, для радиальных составляющий нейтронного потока в цилиндрическом эквивалентном реакторе будем иметь

(4.2.24)

здесь Ф₁, Ф₂, Ф₃… Ф_m – спектр нейтронов, полученный в итерационном расчете;ξ₀–первый корень функции Бесселя первого рода нулевого порядка.

Аналогичного для распределения потоков нейтронов в (r,z) - геометрии для цилиндрического реактора

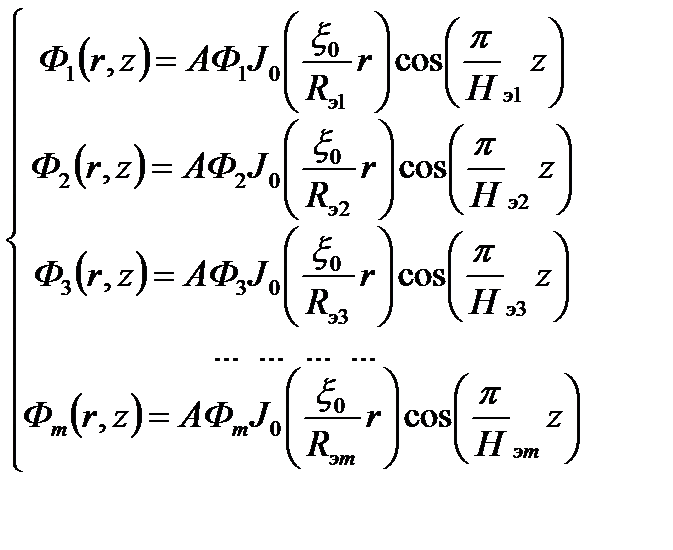
Константа A введена для перевода плотностей потоков в абсолютные единицы путем нормировки на удельную мощность реактора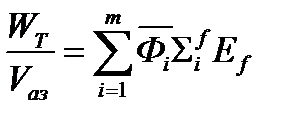

где W_T – тепловая мощность реактора;

E_f = 3,2*10^-11 Дж/дел – энергия, выделяющаяся в одном акте деления.

Среднее значение потока нейтронов для каждой группы определятся по теореме о среднем

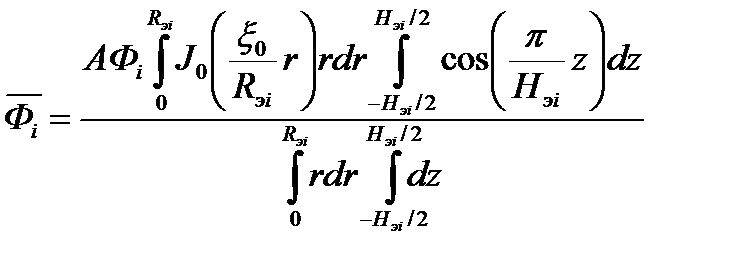(4.2.25)

4.3. Выбор числа групп и особенности подготовки многогрупповых констант.

Выбор числа групп определяется многими факторами, главными из которых является вид спектра нейтронов и требуемая точность вычислений.

Очевидно, что при малом количестве групп, а соответственно, при большой энергетической ширине каждой из них, проблему составляет потеря точности при усреднении параметров внутри группы.

Существует определенность в самой нижней по энергии (большой по номеру) тепловой группе. Здесь распределение плотности числа нейтронов по энергии соответствует Максвелловскому и усреднение параметров не представляет большой сложности.

В нескольких самых верхних поэнергии (начальных по номеру) группах предполагается, что энергетическое распределение нейтронов соответствует спектру деления (спектр Уатта), что также вносит какую-то определенность для усреднения.

Наиболее проблематична область промежуточных энергий при описании замедляющихся нейтронов.

Логично предположить, что здесь нейтроны распределены по спектру Ферми, но усреднение в широком энергетическом интервале значительно искажает закономерности резонансного взаимодействия нейтронов.

При усреднении резонансы полностью сглаживаются. А влияние узких резонансов вообще пропадает.

В усредненных по широкому энергетическому интервалу параметра пропадает влияние эффекта Доплера (расширение резонансного пика при увеличении температуры среды)

Логичным при такой ситуации является уменьшение ширины энергетических групп (увеличение числа групп) для повышения точности при усреднении параметров внутри группы.

Однако, при чрезмерном уменьшении ширины энергетических интервалов наблюдается обратный эффект –рост погрешности.

Причина заключается в следующем.

В системе групповых уравнений сечение увода (Σ_ув=Σ_а+Σ_з) выполняет ту же роль, что и сечение поглощения в уравнении диффузии.

При большом числе «узких» групп их ширины Δu_i малы и соизмеримы со средними логарифмическими потерями энергии в процессе рассеяния (Δu_i~ξ). Это означает, что практически любое столкновение нейтрона приводит к его уводу их группы либо за счет замедления, либо за счет поглощения.

Таким образом, при уменьшении ширины группы резко возрастает количество центров потерь (увода) нейтронов.

Для диффузионных уравнений необходимо увеличивать диапазон летаргии относительно средних логарифмических потерь.

Таким образом, возникает противоречие: увеличение числа групп улучшает качество усредненных групповых параметров, но ухудшает точность диффузионного описания переноса нейтронов.

И наоборот: уменьшение числа групп положительно влияет на применимость диффузионного приближения, но существенно ухудшает точность групповых параметров, получаемых при их усреднении внутри широкого энергетического интервала.

В связи с этим применяют следующий подход:

На первом этапе рассматривают многогрупповую систему уравнений (26, 64, 128 и т.д. групп). Определяют необходимые групповые константы.

Затем сворачивают некоторое число смежных групп в одну более широкую, получая «малогрупповую» систему уравнений, из которых находят пространственное распределение нейтронных потоков и условие критичности.

Выбор числа групп, к которым переходят при свертке констант, опять определяется спектром нейтронов.

Если в ядерном реакторе спектр изменяется слабо или известен закон его изменения, то можно использовать малое число групп.

Например, для расчетов реакторов на тепловых нейтронах наиболее часто многогрупповые константы сворачивают в две группы.

Хотя для водо-водяных реакторов (ВВЭР) более корректным является 4-х групповое приближение.

Для реакторов на быстрых и промежуточных нейтронах требуется рассматривать большее число групп для детализации нейтронных потоков в области резонансных энергий.

4.3. Свертка многогрупповых констант для малогрупповых приближений. Многогрупповое уравнение для ценности нейтронов и его решение