Экстремумы с помощью первой производной
Рассмотрим данное правило на примере: 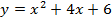
1. Находят производную функции: 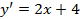 .
.
2.Находят критическое значение аргумента, для чего 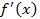 приравнивают к нулю и получают действительные корни уравнения (если корни уравнения мнимые, то экстремума нет).
приравнивают к нулю и получают действительные корни уравнения (если корни уравнения мнимые, то экстремума нет).
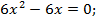
| |
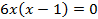
| |

| - критические точки |
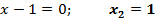
|
3. Критические значения аргумента располагают в возрастающем порядке. Определяют знаки производной для значений аргументов, расположенных правее и левее и близких к критическим точкам. Если знак производной меняется с (-) на (+), то данное значение аргумента является точкой минимума, если знак производной меняется с (+) на (-), то данное значение аргумента является точкой максимума.
| |||
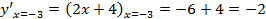
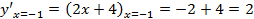
|
Знак производной изменился при переходе через критическую точку с (-) на (+), значит точка 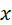 =-2 – это точка минимума.
=-2 – это точка минимума.
4. Вычисляют значение функции в точках максимума и минимума: Ymax, Ymin.
В нашем случае:
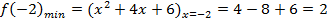
Данное правило исследования функции на экстремумы можно представить в виде следующей таблицы:
| Критическое значение аргумента | Знаки производной 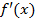 , при переходе через критическую точку х=х0 , при переходе через критическую точку х=х0
| Характер критической точки | 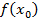
| ||
| х0 | x<х0 | х=х0 | x>х0 | ||
| x1 x2 x3 x4 | - + - + | + - - + | Min Max Нет экстремума Нет экстремума | 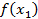 min min
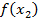 max max
|
Дата добавления: 2016-06-05; просмотров: 2440;











