Необходимые и достаточные условия возрастания и убывания дифференцируемой функции на интервале.
Теорема: Если дифференцируемая функция 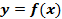 возрастает в данном интервале ]a, b[, то в любой точке этого интервала
возрастает в данном интервале ]a, b[, то в любой точке этого интервала 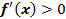 ,
,
Если дифференцируемая функция 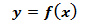 убывает в данном интервале ]a, b[, то в любой точке этого интервала
убывает в данном интервале ]a, b[, то в любой точке этого интервала 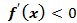 ;
;
Если дифференцируемая функция 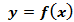 не изменяется в данном интервале ]a, b[, то в любой точке этого интервала
не изменяется в данном интервале ]a, b[, то в любой точке этого интервала 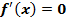 .
.
Интервалы, на которых функция возрастает [убывает], называются интервалами монотонности функции.
Если производная 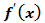 функции
функции 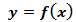 непрерывна, то разделять интервалы монотонности могут лишь точки, в которых
непрерывна, то разделять интервалы монотонности могут лишь точки, в которых 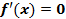 , т. к. перемена знака непрерывной функции возможна лишь при переходе производной функции через нуль.
, т. к. перемена знака непрерывной функции возможна лишь при переходе производной функции через нуль.
Теорема: Если производнаяs w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 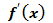 функции
функции 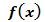 на интервале ]a, b[ положительна, то функция
на интервале ]a, b[ положительна, то функция 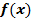 на этом интервале строго возрастает.
на этом интервале строго возрастает.
Если производная 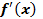 функции
функции 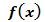 на интервале ]a, b[ отрицательна, то функция
на интервале ]a, b[ отрицательна, то функция 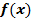 на этом интервале строго убывает.
на этом интервале строго убывает.
Если производная 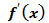 функции
функции 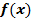 на интервале ]a, b[ равна нулю, то функция
на интервале ]a, b[ равна нулю, то функция 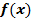 на этом интервале не изменяется.
на этом интервале не изменяется.
Дата добавления: 2016-06-05; просмотров: 3456;











