Правило исследования дифференцируемой функции на возрастание и убывание
Разберем это правило на примере:
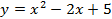
1. Находим производную данной функции. Точки 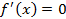 разбивают область определения функции
разбивают область определения функции 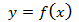 на интервалы, в каждом из которых производная функции
на интервалы, в каждом из которых производная функции 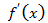 сохраняет знак.
сохраняет знак.
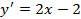
Приравниваем производную к нулю:
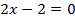
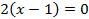
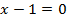
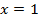
На числовой оси получаем два промежутка монотонности:ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
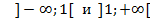 .
.
2. Исследуется знак 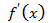 на каждом интервале.
на каждом интервале.
Функция возрастает, если 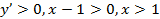 .Т. о. в интервале
.Т. о. в интервале 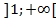 функция возрастает.
функция возрастает.
Функция убывает, если 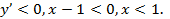 Т. о. в интервале
Т. о. в интервале
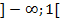 функция убывает.
функция убывает.
ЭКСТРЕМУМЫ ФУНКЦИЙ
Рассмотрим график произвольной функции 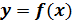
| ||||||||||
| Рис 3. Экстремумы функции. |
Точка А – точка минимума. Точка В – точка максимума.
Если существует такая двухсторонняя окрестность точки x0, что для всякой точки х≠х0 этой окрестности имеет место неравенство
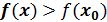 ,то точка
,то точка 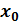 называется точкой минимума функции
называется точкой минимума функции 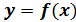 ,а число
,а число 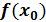 –минимумом функции
–минимумом функции 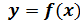 .
.
Если для всякой точки х≠х1 некоторой окрестности точки 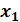 выполняется неравенство
выполняется неравенство 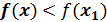 ,то точка
,то точка 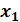 называется точкой максимума функции
называется точкой максимума функции 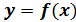 ,а число
,а число 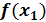 –максимумом функции.
–максимумом функции.
Точка минимума или максимума называется точкой экстремума, а максимум или минимум функции – экстремумом функции.
Дата добавления: 2016-06-05; просмотров: 2154;











