ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

<8 9 101112 13 14 >

Процесс дифференцирования, т.е. нахождение производной или дифференциала функции, с физической точки зрения сводится к следующему: зная закон движения материальной системы, определить мгновенное значение скорости в данной точке траектории её движения. С геометрической точки зрения, этот процесс состоит в нахождении tga угла наклона касательной, проведённой к графику функции в данной точке.

Но часто ставится и обратная задача, т. е. необходимо определить закон движения материальной системы, зная её скорость, или по tga угла наклона касательной найти соответствующую функцию. Для решения этой задачи вводится понятие неопределённого интеграла, а сам процесс решения называется интегрированием.

Другими словами: если процесс дифференцирования состоит в нахождении производной данной функции, то процесс интегрирования - это нахождение функции по её производной или дифференциалу.

Найти интеграл значит найти первообразную функции F(х) и сложить её с произвольной постоянной интегрирования С:

.

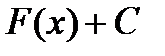Таким образом, каждый неопределенный интеграл имеет бесчисленное множество решений или семейство первообразных.

Функция F(x), имеющая функцию f(x) своей производной или f(x)dx своим дифференциалом, называется первообразной данной функции:

;

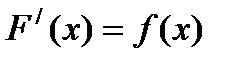dF(x) = f(x) dx.

Неопределенный интеграл в общем виде записывается:

,

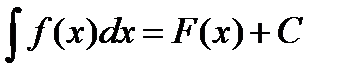где ∫-знак неопределённого интеграла,

f(x) - подинтегральная функция,

f(x)dx - подинтегральное выражение,

F(x) – первообразная функция

С – произвольная постоянная интегрирования

F(x)+С–решение неопределенного интеграла или семейство первообразных.

<8 9 101112 13 14 >

Дата добавления: 2016-06-05; просмотров: 1806;

Поиск по сайту

Узнать еще