Алгоритм решения задач с помощью теоремы
Об изменении кинетической энергии СМТ – схема
Алгоритма Д49 КЭС с комментариями и примерами
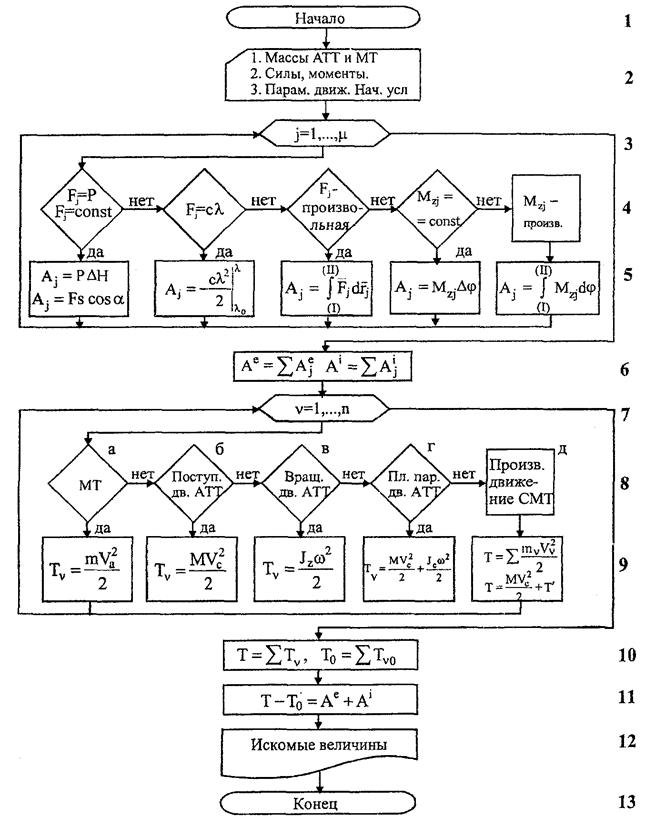
Комментарии
К.2.Рассматриваемый объект принимается за МC. Выделяются и нумеруются МТ и НМС, входящие в МC. На чертеже изображается силовая схема, т.е. рисуются все внешние силы и моменты, действующие на МC, в том числе внешние пассивные силы – силы реакций связей и реактивные моменты на основании принципа освобождаемости от связей (аксиома 5 статики). Если МС не является НМС, то в этом случае в силовую схему должны быть включены внутренние силы.
К.5,9.Все перемещения, необходимые для подсчета работы, и все скорости (линейные, угловые), необходимые для подсчета кинетической энергии, выражаются либо через те, которые заданы, либо через те, которые необходимо определить (в зависимости от числа степеней свободы МС).
Связь между перемещениями и между скоростями в зависимости от вида движений устанавливается с помощью соотношений, приведенных в Ч.1 Кинематика.
К.6.В случае, если МС является НМС, работа внутренних сил – Аi будет равна нулю.
К.8а,9а.При подсчете кинетической энергии МТ, находящейся в сложном движении, необходимо помнить, что на основании теоремы о сложении скоростей в сложном движении 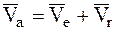 (Ч.1 Кинематика).
(Ч.1 Кинематика).
К.8б,9б.Аналогичной формулой выражается кинетическая энер-гия МС, скорости всех точек которой равны (лента, трос, цепь).
К.9в,г. Моменты инерции определяются с помощью формул, приведенных в таблице 2.
К.9д.Первое соотношение представляет собой общую формулу кинетической энергии МС. Второе соотношение является теоремой Кенига (4.43), причем 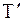 - это кинетическая энергия МС в ее относительном движении по отношению к поступательно движущейся системе координат с началом отсчета в центре масс.
- это кинетическая энергия МС в ее относительном движении по отношению к поступательно движущейся системе координат с началом отсчета в центре масс.
К.10. Кинетическая энергия считается для начального и текущего или заданного моментов времени.
К.11.Для решения задач, связанных с ускорениями и мощностями, могут быть использованы две дифференциальные формы этой теоремы: 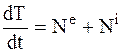 ,
, 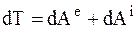 .
.
В этом случае мощности внешних – Ne и внутренних – Ni сил определяются по формулам, аналогичным формулам, приведенным в процессе 5, только вместо перемещений записываются скорости (линейные, угловые).
Если МС является НМС, работы и мощности внутренних сил равны нулю и теорема об изменении кинетической энергии примет следующий вид (три формы):
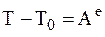 ,
, 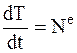 ,
, 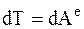 .
. 
Пример 1
2 К грузу 1 массы m1 и цилиндрическому катку 3 радиуса r массы m3 прикреплена нить, переброшенная через блок 2 массы m2 (рис. 38).
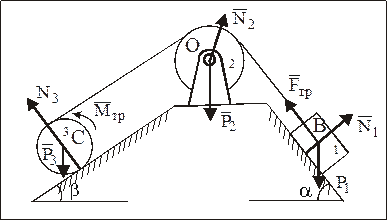
Рис. 38
Определить скорость груза 1 в зависимости от пройденного им вниз по наклонной плоскости пути s и условие того, чтобы груз опускался, если в начальный момент система находилась в покое. Блок 2 и каток 3 считать однородными круглыми цилиндрами, массой нити пренебречь. Коэффициент трения скольжения груза – fc , а коэффициент трения качения катка – fk.
МС состоит из одной МТ – груза 1 и двух АТТ – блока 2 и катка 3.
 3 µ=8.
3 µ=8.
j=1
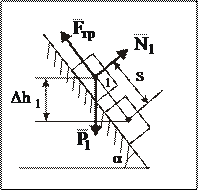
4 Работа силы тяжести 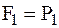 .
.
5 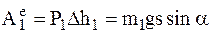 .
.
j=2
4 Работа силы тяжести F2 = P2.
 5
5 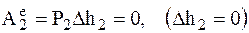 .
.
j=3
4 Работа силы тяжести F3 = P3.
5. 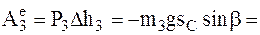
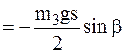 , здесь
, здесь 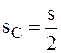 .
.
j=4
4 Работа силы трения скольжения F4 = Fтр.
5 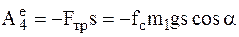 , здесь
, здесь 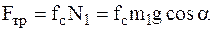 .
.
j = 5
4 Работа момента трения качения 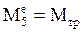
5 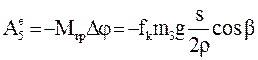 ,
,
Здесь 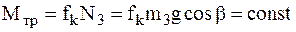 ,
, 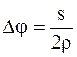
j = 6,7,8
4 Работа нормальных сил реакции.
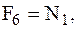
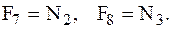
5 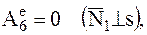
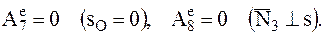
6 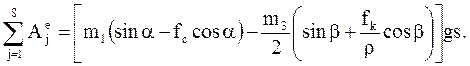
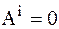 .
.
7n=3.
n = 1
8а Движение МТ – груза 1. 9а 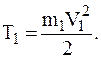
n = 2
8в Вращательное движение АТТ – блока 2 .
9в 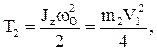 здесь
здесь 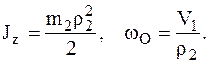
n = 3
8гПлоскопараллельное движение АТТ – катка 3 .
9г 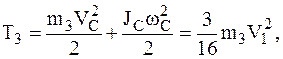
здесь 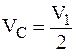 ,
, 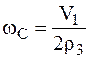 ,
, 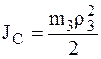
10 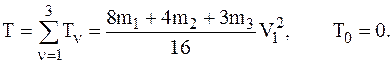
11 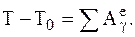
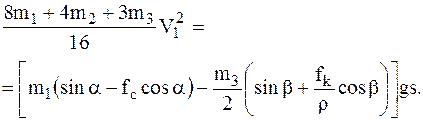
12Ответ: 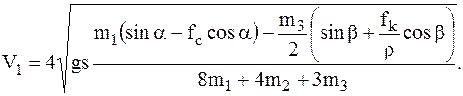
Условие того, чтобы груз 1 опускался: V1 > 0, т. е.
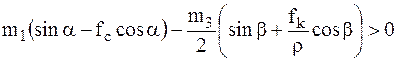 .
.
Дата добавления: 2016-06-05; просмотров: 2082;











