Пряма лінія в просторі.
Одна з аксіом Евкліда постулює: через дві різні точки проходить пряма і тільки одна. В аналітичній геометрії цій аксіомі відповідає канонічне рівняння прямої, що проходить через дві задані точки:
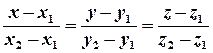 ;
;
тут 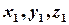 і
і 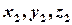 — координати відповідних точок.
— координати відповідних точок.
Зрозуміло, що не для всякої прямої можна скласти канонічне рівняння: якщо хоча б одна пара відповідних координат у точок співпадає, то принаймні один знаменник буде дорівнювати 0. В той же час будь-яка пряма лінія в просторі може бути задана загальним рівнянням. Тільки це рівняння не є рівнянням у буквальному розумінні цього терміну. Отже, загальне рівняння прямої в просторі:
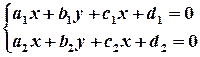 .
.
Загальне рівняння, як бачимо, є не рівнянням, а системою двох рівнянь. Кожне рівняння визначає площину в просторі. Це означає, що загальне рівняння визначає пряму лінію в просторі як лінію перетину двох площин.
Якщо придивитись до канонічного рівняння прямої, то можна сказати, що це також, в принципі не є рівнянням, бо в ньому є два знака рівності. То ж виникають, наприклад, такі питання: як перейти від канонічного рівняння до загального і, навпаки, від загального до канонічного? Пропонуємо ці питання для самостійного обмірковування для конкретних заданих прямих:
Вправа 1. Перейти від канонічного рівняння прямої

До загального.
Вправа 2. Перейти від загального рівняння прямої
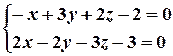
До канонічного.
Вправа 3. Скласти канонічне і загальне рівняння прямої, що проходить через точки 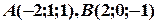 .
.
Вправа 4. Вказати координати двох точок, що належать прямій
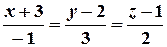 .
.
1.7. „За числами бачити фігури”.
Розглянемо просту задачу, яка яскраво ілюструє цю ідею.
Задача. Знайти найбільше значення параметра 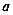 , при якому система
, при якому система
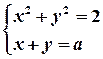
Має два розв’язки.
Нашого знайомства з методом координат вже достатньо для того, щоб побачити за першим рівнянням системи коло з центром у початку координат, а за другим рівнянням – пряму, що проходить через точки 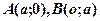 . Отже, алгебраїчна задача еквівалентна геометричній задачі: при якому найбільшому значенню параметра
. Отже, алгебраїчна задача еквівалентна геометричній задачі: при якому найбільшому значенню параметра 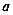 вказані коло і пряма перетинаються у двох точках? Переходимо до малюнку:
вказані коло і пряма перетинаються у двох точках? Переходимо до малюнку:
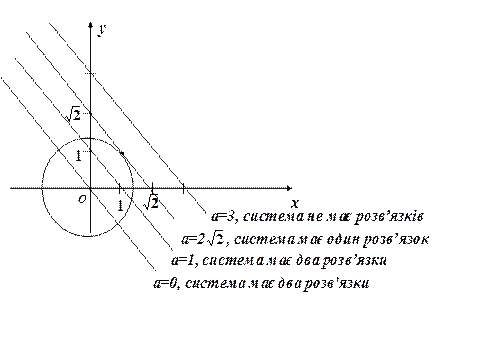
Що можна сказати, аналізуючи малюнок? Можна сказати, що найбільше значення параметру 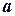 , при якому коло і пряма перетинаються, відповідає значенню параметра
, при якому коло і пряма перетинаються, відповідає значенню параметра 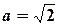 . Якщо
. Якщо 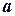 зменшити на будь-яке, хоча б і дуже маленьке число, точок перетину у кола і прямої буде вже 2. Отже ... (остаточний висновок і відповідь зробіть і дайте самостійно).
зменшити на будь-яке, хоча б і дуже маленьке число, точок перетину у кола і прямої буде вже 2. Отже ... (остаточний висновок і відповідь зробіть і дайте самостійно).
Вправа. Знайти найбільше значення параметра 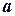 , при якому система
, при якому система
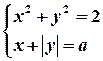
Має два розв’язки.
Дата добавления: 2021-05-28; просмотров: 624;











