Ділення відрізка у даному відношенні.

Формула ділення відрізка в заданому відношенні грунтується на теоремі Фалеса: якщо дві дані прямі перетнути трьома (або більшою кількістю) паралельних прямих, то відношення довжин відрізків, що відтинаються цими паралельними прямими на одній з даних прямих, дорівнює відношенню довжин відповідних відрізків на другій з даних прямих.

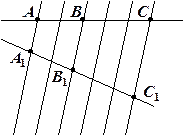
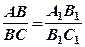
Розглянемо задачу ділення заданого відрізку прямої на координатній площині на 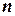рівних частин. Це означає: за заданими координатами кінців відрізку 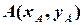, 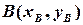(розглядаємо задачу для випадку площини) знайти координати точок ділення 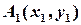, , 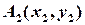…, , 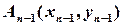так що

.

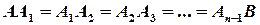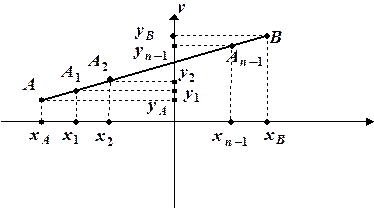
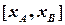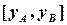Виходячи з теореми Фалеса, відрізки та , які є проекціями даного відрізку на координатні осі, також поділені на 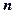рівних частин. Отже,

,

.

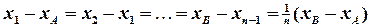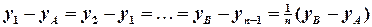Звідси,

, ;

, .

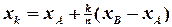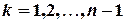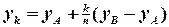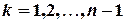Остаточно маємо координати точок ділення:

,

,

………………………

,

………………………

.

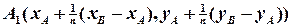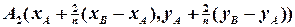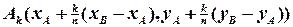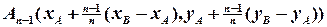Тепер розглянемо задачу ділення заданого відрізку прямої на координатній площині у заданому відношенні 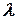. Це означає: за заданими координатами кінців відрізку 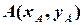, 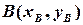знайти координати точки ділення 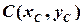цього відрізку так, щоби відношення довжин відрізків 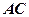та 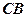дорівнювало :

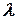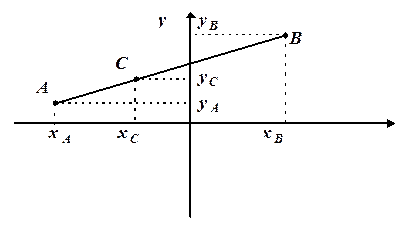
Треба знайти координати точки 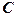, виходячи з того, що відношення довжин відрізків 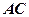та 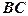має дорівнювати :

.

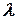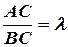Повторюючи міркування з попередньої задачі, маємо:

.

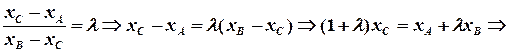
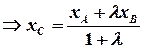Аналогічно отримуємо

.

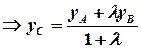Зокрема, якщо треба поділити відрізок 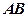навпіл, то точка ділення 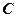буде мати такі координати:

,

.

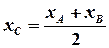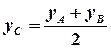Аналогічні формули мають місце для випадку простору.