Первая (прямая) задача динамики

Зная массу и закон движения объекта (точка, тело, система тел)

определить модуль и направление равнодействующей сил, вызывающих это движение.

Дано: m ;

x = f1 (t );

y = f2 (t );

z = f3 (t ).

Определить: R .

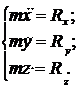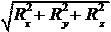
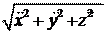R = = m .

Направление вектора R определяется направляющими косинусами:

cosa =

cosa = Rx

R

;

=

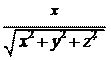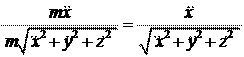cos b =

.

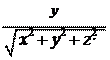
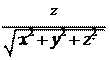; cosg = ,

где a – угол между векторами R и

b – угол между векторами R и

g – угол между векторами R и

Rx , град.;

Ry , град.;

Rz , град.

Вторая (обратная) задача динамики

Зная массу и силы, действующие на объект, а также начальные условия, определить закон его движения.

Дано: m ; R .

Определить:

x = f1 (t );

y = f2 (t );

z = f3 (t ).

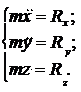
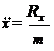
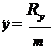
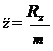; ; . (2.5)

Сила может быть постоянна по модулю и направлению или быть

функцией нескольких переменных точки в пространстве, скорости).

R = f (t,r ,u )

(времени, положения

Проинтегрировав дважды полученные дифференциальные уравнения

(2.5) и определив постоянные интегрирования ( C1 ,

C2 , …,

Cn ), получим

кинематические уравнения движения материальной точки –

x = f1 (t );

y = f2 (t ); z = f3 (t ).