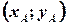Пряма лінія на площині.
Так само, як і точка, пряма лінія в геометрії є неозначуваним поняттям. І так само ми зустрічаємо “означення” прямої в “Началах” Евкліда. Спочатку Евклід визначає поняття лінії: це “довжина без ширини”. Пряма лінія — це “лінія, яка однаково розташована по відношенню до кожної із своїх частин”.
В аналітичній геометрії, тепер, коли ми можемо ототожнити точки з парами чи трійками координат, можна дати означення прямої лінії: пряма — це геометричне місце точок, координати яких задовольняють лінійне рівняння (це означення прямої лінії на координатній площини):
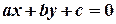 .
.
Наведене рівняння зветься загальним рівнянням прямої і відоме з курсу математики для середньої школи; там же визначалось рівняння прямої з кутовим коефіцієнтом:
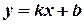 .
.
Параметри 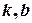 у цьому рівнянні мають такий геометричний зміст:
у цьому рівнянні мають такий геометричний зміст: 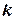 – кутовий коефіцієнт – тангенс кута нахилу прямої до додатного напрямку осі абсцис,
– кутовий коефіцієнт – тангенс кута нахилу прямої до додатного напрямку осі абсцис, 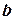 – точка на осі ординат, через яку проходить пряма. Очевидною умовою паралельності прямих є рівність їх кутових коефіцієнтів:
– точка на осі ординат, через яку проходить пряма. Очевидною умовою паралельності прямих є рівність їх кутових коефіцієнтів:
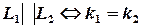
Тригонометрія дає умову перпендикулярності двох прямих. Нехай
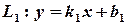 ,
,
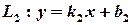
(цей запис говорить, що прямі 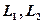 задані відповідними рівняннями), тоді умовою перпендикулярності цих прямих буде такий зв’язок між їх кутовими коефіцієнтами:
задані відповідними рівняннями), тоді умовою перпендикулярності цих прямих буде такий зв’язок між їх кутовими коефіцієнтами:
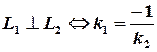
В цьому параграфі ми познайомимось ще з двома типами рівнянь прямої:
— канонічне рівняння прямої, що проходить через дві задані точки
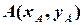 і
і 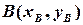 :
:
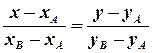 ;
;
— рівняння прямої “у відрізках”:
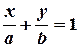 .
.
В цьому рівнянні 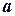 і
і 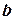 — це відрізки, які пряма відтинає на координатних осях; точніше буде сказати так: дана пряма проходить через точки
— це відрізки, які пряма відтинає на координатних осях; точніше буде сказати так: дана пряма проходить через точки 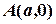 і
і 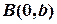 .
.
Поєднаємо тепер геометрію з алгеброю для розв’язання задачі: на даній прямій знайти точку, найближчу до заданої точки. Цю задачу будемо розглядати для конкретних заданих прямої та точки, а саме, нехай пряма лінія 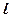 визначається рівнянням
визначається рівнянням 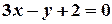 , а задана точка
, а задана точка  має координати
має координати  .
.
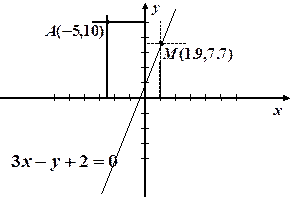
В геометрії аналогом подібних задач, тобто задач на обчислення, є задачі на побудову (циркулем і лінійкою). Першим кроком у розв’язанні таких задач є аналіз, який починається словами: “припустимо, що задача розв’язана”. Далі будується ескізний малюнок, який аналізується щодо можливості побудови відповідної фігури. В аналітичній геометрії ми робимо аналогічне припущення: нехай 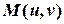 — шукана точка прямої. Підставимо координати точок
— шукана точка прямої. Підставимо координати точок  і
і  у формулу відстані між двома точками:
у формулу відстані між двома точками:
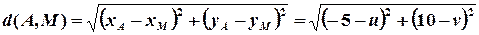 .
.
Координати точки 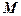 мають задовольняти рівняння прямої, отже
мають задовольняти рівняння прямої, отже
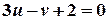 .
.
Звідси можна виразити одну з невідомих координат точки 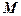 через іншу. В даному випадку доцільніше виразити
через іншу. В даному випадку доцільніше виразити 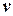 через
через 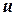 :
:
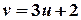 .
.
Підставимо вираз для 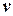 у формулу для
у формулу для 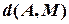 :
:
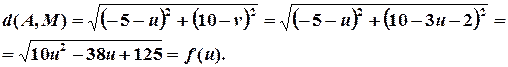
Точка 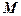 має доставляти мінімум відстані
має доставляти мінімум відстані 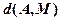 , а отже, і функції
, а отже, і функції 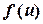 .
.
В математичному аналізі за мінімуми “відповідає” теорема Ферма (§ 19), в аналітичній геометрії ми маємо у розпорядженні геометричні міркування і алгебраїчні перетворення.
Геометричні міркування. Найближча точка від даної на даній прямій – це основа перпендикуляра, опущеного з даної точки на дану пряму. Перетворюємо рівняння даної прямої 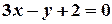 у рівняння з кутовим коефіцієнтом:
у рівняння з кутовим коефіцієнтом: 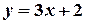 . Кутовий коефіцієнт даної прямої
. Кутовий коефіцієнт даної прямої 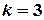 . Кутовий коефіцієнт перпендикулярної прямої
. Кутовий коефіцієнт перпендикулярної прямої 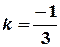 . Рівняння перпендикуляра
. Рівняння перпендикуляра 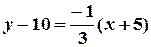 . Знаходимо точку перетину даної прямої і перпендикуляра до неї – розв’язуємо систему рівнянь:
. Знаходимо точку перетину даної прямої і перпендикуляра до неї – розв’язуємо систему рівнянь:
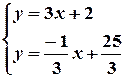
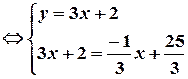
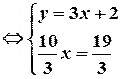 .
.
Звідси
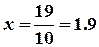 і
і 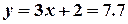 .
.
Отже, найближчою для точки 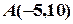 на прямій
на прямій 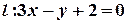 буде точка
буде точка 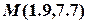 .
. 
Більш складним і цікавим щодо застосування методу координат є задача про визначення місця для побудови водокачки (див. Вступ).
За відправну точку при побудові математичної моделі задачі можна взяти таку аналітико-геометричну задачу: на осі абсцис знайти точку з мінімальною сумою відстаней до заданих точок 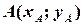 і
і 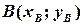 .
.
 y
y
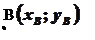 | |||||
| |||||
 | |||||

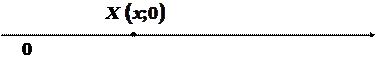 |
|
Далі можна, знову ж таки, йти „простим” шляхом і звести задачу до
знаходження точки мінімуму ірраціональної функції:
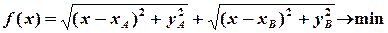 ,
,
для чого застосувати теорему Ферма. Тільки тоді доведеться розв’язувати не таке вже й просте ірраціональне рівняння (див. § 19).
Аналітична геометрія може дуже елегантно розв’язати цю задачу, використовуючи тонкі геометричні міркування:


Побудуємо точку 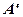 , симетричну
, симетричну 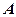 відносно прямої
відносно прямої 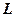 , що визначає лінію берега. З’єднаємо
, що визначає лінію берега. З’єднаємо 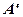 з
з 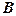 . Шукана точка
. Шукана точка 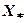 — це точка перетину
— це точка перетину 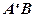 з
з 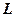 . Стверджується, що ця точка є шуканою (доведення цього факту є вправою для самостійного доведення).
. Стверджується, що ця точка є шуканою (доведення цього факту є вправою для самостійного доведення).
Тепер алгебраїчна реалізація геометричної ідеї:
1) складаємо рівняння перпендикуляра до прямої 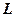 , який проходить через точку
, який проходить через точку 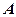 ;
;
2) знаходимо точку перетину перпендикуляра з прямою 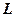 (це буде середина відрізка
(це буде середина відрізка 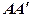 ;
;
3) використовуючи формулу для координат середини відрізка, знаходимо координати точки 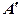 ;
;
4) складаємо рівняння прямої, що проходить через точки 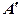 і
і 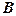 ;
;
5) розв’язуємо систему рівнянь, складену з рівняння даної прямої 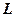 і прямої
і прямої 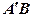 ; отримаємо координати шуканої точки
; отримаємо координати шуканої точки 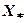 .
.
Дата добавления: 2021-05-28; просмотров: 686;