Поняття вільного вектора.

<5 6 789 10 11 >

Означення (вільного вектора). Вільним вектором називається направлений відрізок прямої, причому якщо два таких відрізка паралельні (колінеарні), однаково направлені і мають однакову довжину ( 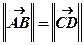), то відповідні вектори вважаються однаковими або рівними між собою.

Поняття довжини вектора вимагає, щоби був заданий масштаб, за допомогою якого звичайним чином вимірюється довжина відрізка, але при цьому воно також вимагає, щоб масштаб був однаковий для всіх векторів.

Словосполучення “направлений відрізок прямої” визначає, так би мовити, геометричний вектор. Для таких векторів суттєвим є їх місцеположення, тобто, де саме знаходиться їх початок та їх кінець. Вільний вектор, на відміну від геометричного вектора, дозволяється пересувати паралельно в будь-яке місце площини чи простору. Можна собі подумки уявити таку картину: до кожної точки площини чи простору “причеплено” вектор, причому всі ці вектори мають однакову довжину, паралельні та співнаправлені. Таким чином, простір виявляється вщент заповненим рівними між собою векторами:

У свою чергу таку картину можна інтерпретувати як перетворення паралельного переносу кожної точки у заданому напрямку на задану відстань.

Тепер, коли поняття вільного вектора введено, відповідно з головним стратегічним принципом методу координат нам треба побудувати аналітичну модель цього поняття. Для цього потрібне поняття проекції вільного вектора на числову вісь.

Означення (проекції вільного вектора на числову вісь). Нехай є вільний вектор 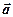і числова вісь 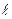, тоді різниця проекцій кінця і проекцій початку зветься проекцією вектора на числову вісь.

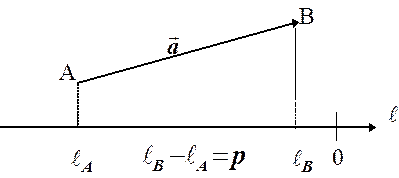
Отже, зрозуміло, що проекція вільного вектора на числову вісь є число і що так введене поняття проекції є коректним: при паралельному пересуванні вектора ані він сам, ані його проекція не змінюються (довести самостійно).

Для подальшого розгляду нам буде потрібний ще один варіант поняття проекціїї вектора. Нехай заданий деякий вектор і дві числові осі. Нехай, до того ж, числові осі паралельні та співнаправлені. Тоді проекції даного вектора на дані осі співпадають (довести самостійно). Отже, фактично, визначальними для проекції вектора на числову вісь є напрямок і масштаб осі. Але вказані компоненти “містяться” у будь-якому векторі, паралельному і співнаправленому з числовою віссю. Наведені міркування пояснюють природність такого поняття проекції вектора:

Означення (проекції вектора на напрямок іншого вектора). Проекцією вектора на напрямок вектора 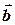називається проекція на будь-яку числову вісь, паралельну і співнаправлену з вектором 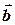; позначення: .

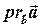Лема (про значення проекції на напрямок).

,

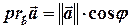де 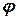— кут між векторами та .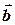

Доведення.Довести самостійно, використовуючи малюнок і геометричні міркування.

Поняття проекції вектора на напрямок іншого вектора буде потрібне при розгляді скалярного добутку векторів.

Означення (координат вектора). Пара (у випадку площини) або трійка (у випадку простору) чисел, які є проекціями даного вектора на координатні осі називаються координатами вектора (відповідно на площині і у просторі).

Теорема (про визначеність вектора своїми координатами). Кожний вектор повністю визначається парою (у випадку площини) або трійкою (у випадку простору) своїх координат; інакше кажучи, два вектори рівні тоді і тільки тоді, коли вони мають рівні відповідні координати.

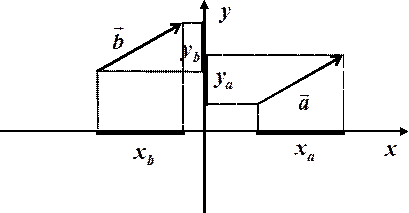
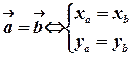(для випадку площини) .

Доведення. Довести теорему самостійно. Вказівка: використати рівність прямокутних трикутників.

Теоремапро визначеність вектора своїми координатами дає підставу ототожнювати вектор з парою (у випадку площини) або трійкою (у випадку простору) його координат:

.

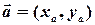Безпосередньо з теореми Піфагора випливає формула для обчислення довжини вектора:

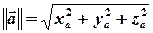(для випадку простору).

Безпосередньо з означення координат вектора і координат точки випливає формула обчислення координат вектора при заданих координатах початку і кінця вектора: нехай 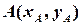і 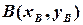довільні точки декартової площини; тоді

.

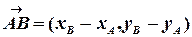Серед усіх векторів є один вектор, який є “не зовсім” вектором, але без якого множина векторів була б логічно не повною. Ситуація щодо цього вектора дуже схожа на ситуацію з числом 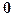(нуль). Вектор, про який йдеться, так і називається: нуль-вектор.Нуль-вектор — це вектор, початок якого співпадає з його кінцем; це вектор довжини нуль; це вектор, всі координати якого дорівнюють нулю:

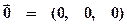(для випадку простору).