Відстань між двома точками. Рівняння кола та сфери.
Формула відстані між двома точками, заданими своїми координатами, безпосередньо випливає з теореми Піфагора:квадрат довжини гіпотенузи прямокутного трикутника дорівнює сумі квадратів довжин його катетів:
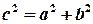
|
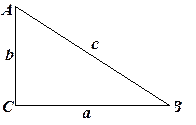
Нехай маємо дві точки на координатній площині:
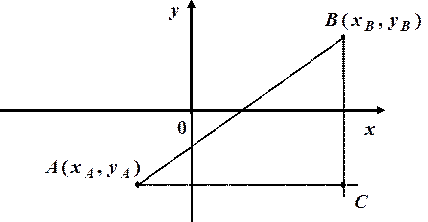
Сполучивши точки 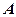 і
і 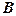 та провівши горизонтальну пряму через точку
та провівши горизонтальну пряму через точку 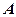 і вертикальну пряму через точку
і вертикальну пряму через точку 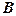 , отримаємо прямокутний трикутник
, отримаємо прямокутний трикутник 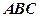 . Довжина гіпотенузи
. Довжина гіпотенузи 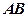 цього трикутника — це відстань між точками
цього трикутника — це відстань між точками 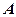 і
і 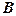 . Довжина катета
. Довжина катета 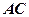 дорівнює
дорівнює 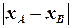 ; довжина катета
; довжина катета 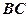 дорівнює
дорівнює 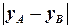 . Позначимо через
. Позначимо через 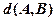 відстань між точками
відстань між точками 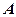 і
і 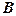 . З теореми Піфагора маємо:
. З теореми Піфагора маємо:
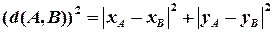 ,
,
звідки випливає формула
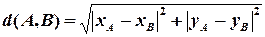
Ця формула дозволяє “перекласти” на аналітичну мову означення кола і сфери. Коло — це геометричне місце точок площини, що розташовані на деякій фіксованій відстані (яка називається радіусом), від деякої фіксованої точки (яка називається центром). Нехай заданий радіус дорівнює 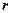 , центром кола є точка
, центром кола є точка 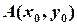 , а “біжучою” точкою кола є
, а “біжучою” точкою кола є 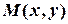 .
.
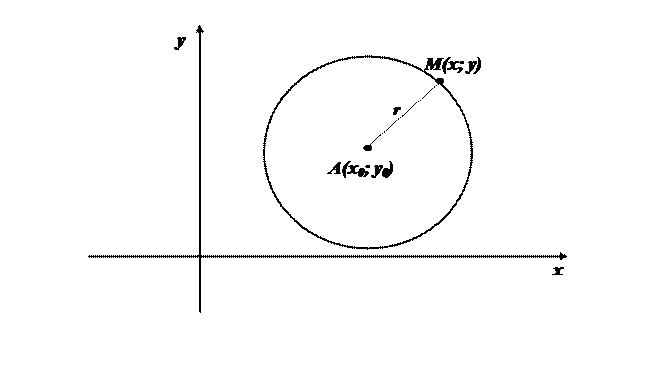
Тоді, з використанням формули відстані між двома точками, означення кола перейде у рівняння:
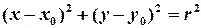 .
.
Аналогічні формули мають місце для тривимірного простору. А саме, якщо 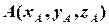 та
та 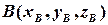 —задані просторові точки, то відстань
—задані просторові точки, то відстань 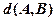 між ними обчислюється за формулою:
між ними обчислюється за формулою:
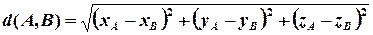 .
.
Для виведення цієї формули замість прямокутного трикутника треба розглядати прямокутний паралелепіпед та його діагональ.
Якщо в означенні кола замінити слово площини на слово простору, — ми отримаємо означення сфери та її рівняння:
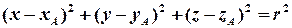 .
.
Дата добавления: 2021-05-28; просмотров: 720;











