Нехай маємо три площини

<4 5 678 9 10 >

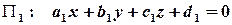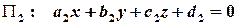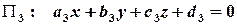Знаходження точки перетину площин зводиться до розв’язання СЛР, складеної з рівнянь цих площин, тобто квадратної СЛР з трьох рівнянь з трьома змінними

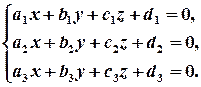
Далі ми будемо робити аналогічні перетворення, як і для СЛР 2х2, тобто такі, які виключають з рівнянь певну змінну. В результаті будуть отримані формули Крамера і сформульоване правило Крамера, які цілком аналогічні формулам і правилу Крамера для СЛР 2х2. Перед виконанням перетворень перенесемо вільні члени в праву частину рівнянь, перепозначивши їх (для позбавлення знаків „-”) іншими буквами:

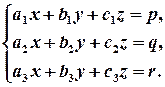
За допомогою 1-го рівняння виключаємо змінну х з 2-го і 3-го рівнянь перетвореннями:

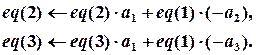
Маємо:

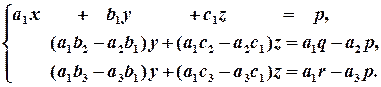
Друге і третє рівняння не містять змінної х (точніше х , входить у ці рівняння з коефіцієнтом 0) і утворюють СЛР 2х2 від у і z , до якої можна застосувати формули Крамера:

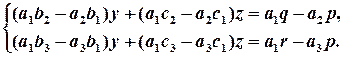
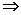
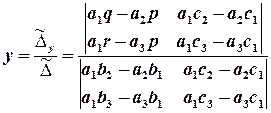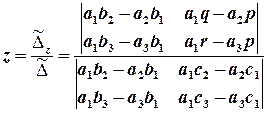Розглянемо вираз у знаменниках дробів. Це визначник 2-го порядку, розкриваємо його за означенням, отримуємо:

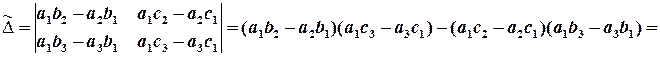
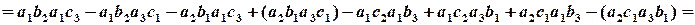
дужками виділені доданки, які взаємно знищуються; маємо:

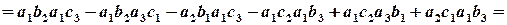
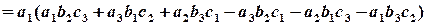Так само розкриваємо визначники 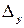і 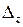– в чисельниках.

Вправа. Отримати розгорнуті вирази для 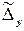і 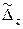і переконатись у вірності виразів:

,

.

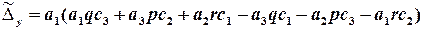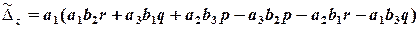Маємо:

, ,

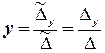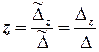де

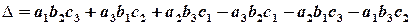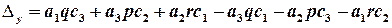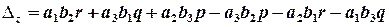Вправа. Підставити отримані вирази для y та z у перше рівняння СЛР 3х3 , виконати необхідні перетворення й переконатись у вірності виразу:

,

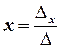де

.

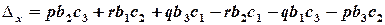Вирази для 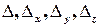мають однакову алгебраїчну структуру, вони отримані за однією й тією самою схемою, причому складаються з елементів квадратних таблиць – квадратних матриць 3-го порядку:

,

,

,

.

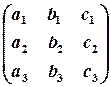
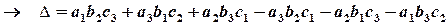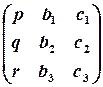
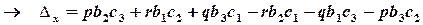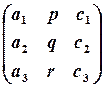
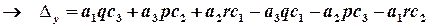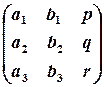
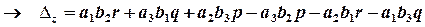Бачимо, що кожний вираз є алгебраїчною сумою шести доданків; кожний доданок є добутком трьох елементів матриці; три добутки беруться з їх знаками, три – з протилежними; які саме елементи утворюють добутки, і які добутки з якими знаками беруться, ілюструє така схема:

Означення (визначника 3-го порядку).

Визначником (або детермінантом) 3-го порядку, тобто визначником квадратної матриці 3х3

,

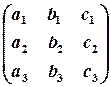позначення:

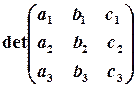або ,

називається число, обчислене за формулою

.

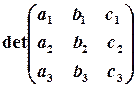
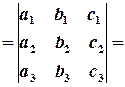
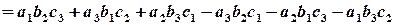Нехай маємо квадратну СЛР розмірів 3х3, тобто СЛР, що складається з 3-х рівнянь від 3-х змінних

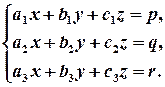
Визначник, складений з коефіцієнтів при невідомих, називається основним визначником СЛР, визначники, отримані заміною в основному визначнику певного стовпчика на стовпчик вільних членів, називаються допоміжними визначниками СЛР.

Проведені міркування і виконані перетворення є доведенням теореми:

Теорема Крамера (для СЛР 3х3). Якщо основний визначник СЛР відмінний від нуля, то СЛР має, і до того ж єдиний, розв’язок, який можна обчислити за формулами Крамера:

,

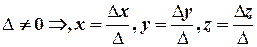де

, , , .

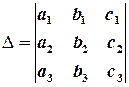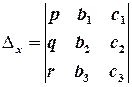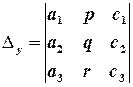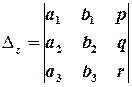Приклад. Знайдемо точку перетину площин

,

,

.

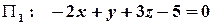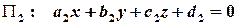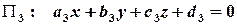Складаємо СЛР, вільні члени одразу переносимо в праві частини рівнянь:

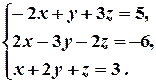
З’ясовуємо можливість застосування правила Крамера (основний визначник СЛР має бути відмінний від нуля):

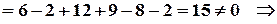правило Крамера можна застосувати.

Обчислюємо допоміжні визначники:

,

, .

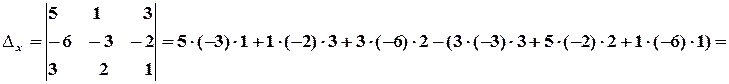
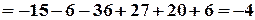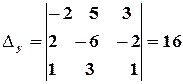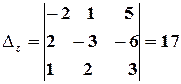За формулами Крамера :

, , .

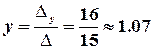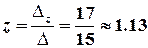Перевірка (підставляємо знайдені значення змінних в кожне рівняння) :

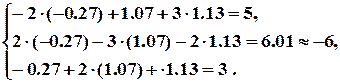
Перевірка підтвердила правильність виконаних обчислень, отже точкою перетину площин є точка .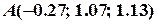

<4 5 678 9 10 >

Дата добавления: 2021-05-28; просмотров: 368;