Пряма і площина в просторі.

Для прямої і площини в просторі є два важливих питання для з’ясування: чи вони паралельні, чи перетинаються, і чому дорівнює відстань між паралельними прямою і площиною? Отже, нехай маємо пряму лінію, задану канонічним рівнянням

,

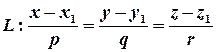і площину, задану загальним рівнянням

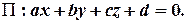
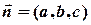– направляючий вектор прямої, – нормальний вектор площини. Очевидно,

.

Таким чином, маємо критерій паралельності прямої і площини:

.

Цілком очевидний також критерій перпендикулярності прямої і площини:

.

Нехай маємо випадок паралельності прямої і площини. З канонічного рівняння отримуємо координати точки, що належить прямій, і далі залишається скористатися формулою відстані між точкою і площиною (п.7.2).

Вправа. Завершити виведення остаточної формули відстані між паралельними прямою і площиною.

Площі.

Основою для обчислення площ лінійних фігур (многокутників) є векторний добуток векторів (див.§5): його геометричний зміст і формула координатного подання. Довжина векторного добутку дорівнює площі паралелограма, побудованого на векторах-множниках як на суміжних сторонах. Звідси безпосередньо отримуємо формулу площі просторового трикутника, заданого координатами своїх вершин. Отже, нехай 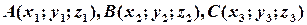– вершини трикутника. Тоді

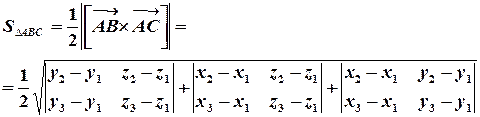
Площа будь-якого многокутника обчислюється, використовуючи цю формулу і розбиттям многокутника на трикутники – так званою триангуляцією многокутника.

Об’єми.

Основою для обчислення об’ємів многогранників є змішаний добуток векторів (див.§6): його геометричний зміст і формула координатного подання. Змішаний добуток векторів за абсолютною величиною дорівнює об’єму паралелепіпеда, побудованого на векторах-множниках як на суміжних ребрах. Звідси безпосередньо отримуємо, наприклад, формулу об’єму піраміди, заданої координатами своїх вершин. Отже, нехай 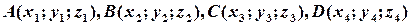– вершини піраміди. Тоді

Подібно до обчислення площ многокутників їх тріангуляцією об’єми многогранників обчислюються розбиттям їх на піраміди.