Пример 2. Прямая задача расчета разветвленной магнитной цепи
(расчет магнитных потоков и индукций по заданной геометрии магнитной системы и намагничивающих силах катушек).
Для магнитной системы изображенной ниже известны: МДС обмоток, сечения участков магнитопровода, длины средних линий участков, кривая намагничивания материала магнитопровода представлена на графике. Требуется рассчитать магнитные потоки в стержнях магнитопровода. Магнитная система имеет следующие параметры:
- сечения участков магнитопровода 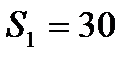 см2 ,
см2 , 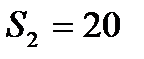 см2 ,
см2 , 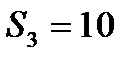 см2 ;
см2 ;
- длины средних линий участков 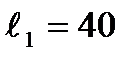 см,
см, 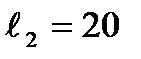 см
см 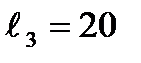 см ;
см ;
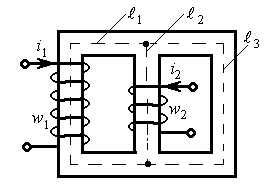
Данная магнитная система может быть представлена в виде магнитной цепи,схема которой имеет вид
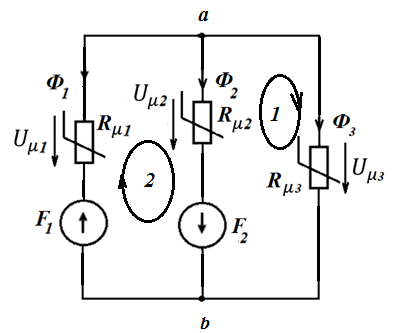
По аналогии с нелинейными электрическими цепями для расчета этой нелинейной магнитной цпи можно использовать все методы расчетов нелинейных электрических цепей. Используем в качестве расчетного графический метод. Для этого необходимо иметь вебер – амперные характеристики (ВАХ) нелинейных магнитных сопротивлений 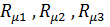 ВАХ – это зависимость магнитного потока от магнитного напряжения на магнитном сопротивлении
ВАХ – это зависимость магнитного потока от магнитного напряжения на магнитном сопротивлении 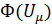 . Эти характеристики могут быть получены по кривой намагничивания ферромагнитного сердечника В(Н), которая в данной задаче представлена в виде графика.
. Эти характеристики могут быть получены по кривой намагничивания ферромагнитного сердечника В(Н), которая в данной задаче представлена в виде графика.
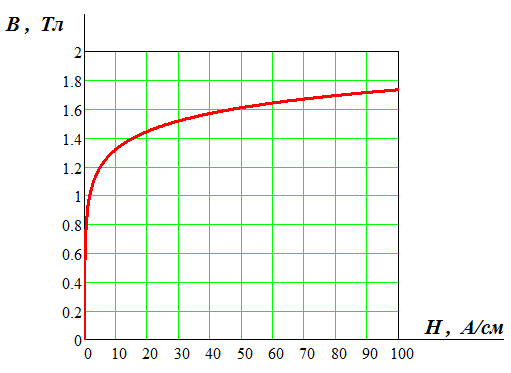
Для получения ВАХ нелинейных магнитных сопротивлений необходимо значения магнитной индукции кривой B(H) ожить на сечение участка, а соответствующие индукции значения напряженности магнитного поля умножить на длину средней линии участка, то есть
 .
.
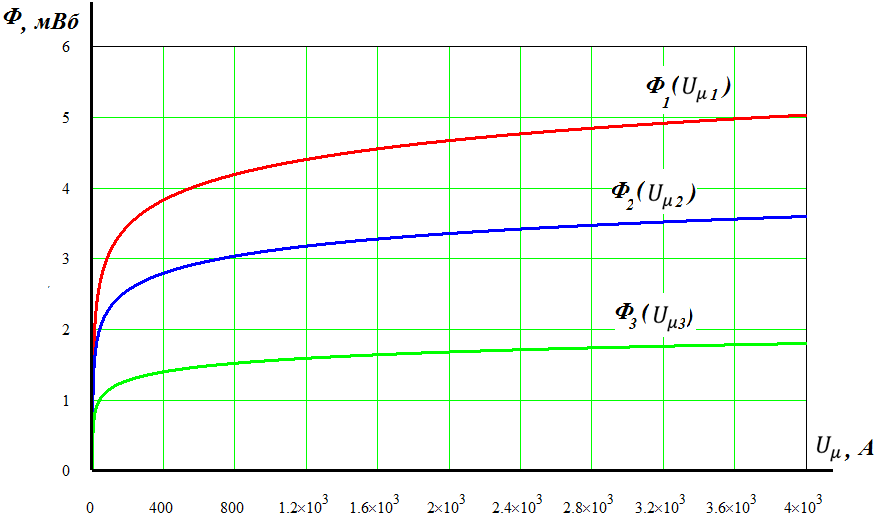
ВАХ нелинейных магнитных сопротивлений в данной задаче после процедуры умножений имеют вид
Для данной задачи графический расчет будем применчть на основе метода узловых потенциалов. В литературе по ТОЭ этот расчет называют методом двух узлов. Особенность метода заключается в выборе направлений стрелок магнитных потоков в ветвях схемы. Стрелки направляются либо в один из узлов, либо к нему. В качестве аргумента функций потоков вместо магнитных напряжений на сопротивлениях, предлагается использовать магнитное напряжение между узлами схемы a и b. Это связано с тем, что это напряжение яляется одинаковым для каждого потока ветвей, поскольку ветви к узлам a и b подключены параллельно.. Пересчет аргумента для ВАХ нелинейных сопротивлений проводится в соответствии со вторым законом Кирхгофа:
для первой ветви 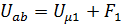 ,
,
для второй ветви 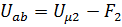 ,
,
для третьей ветви 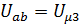 .
.
Графики зависимостей потоков от магнитного напряжения 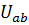 приведены ниже .
приведены ниже .
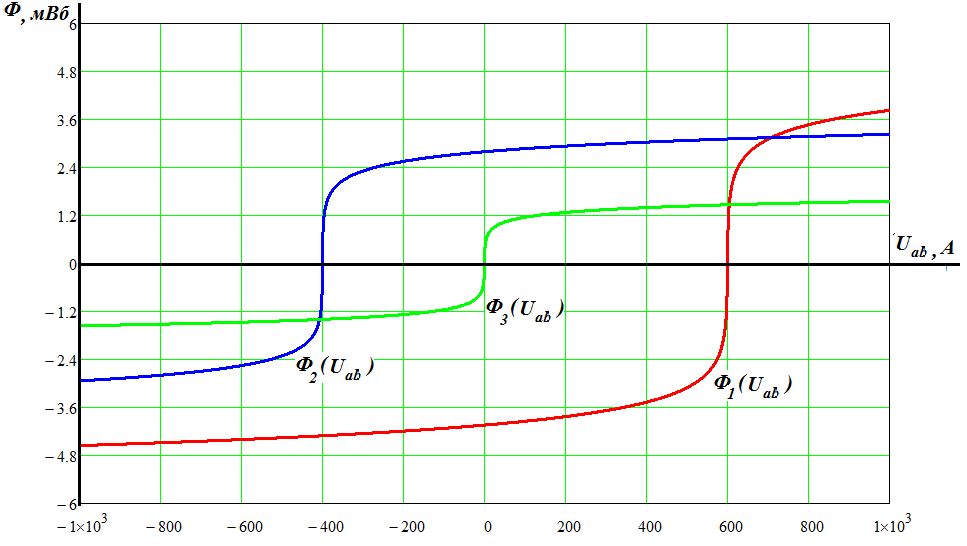
Как видно из графиков их построение можно провести, смещая ВАХ нелиейных магнитных сопротивлений по оси магнитного напряжения в зависимости от величины и направления МДС в ветвях цепи. Если направление стрелки МДС совпадает со стрелкой потока, то ВАХ смещается влево по оси напряжений на величину F, в противном случае ВАХ смещается вправо. Для данной задачи ВАХ магнитного сопротивления 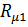 смещена вправо на величину
смещена вправо на величину 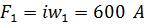 по оси
по оси  , а ВАХ магнитного сопротивления
, а ВАХ магнитного сопротивления 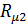 смещена влево на величину
смещена влево на величину 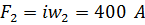 по оси
по оси 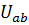 . ВАХ магнитного сопротивления
. ВАХ магнитного сопротивления 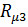 не смещается по оси
не смещается по оси 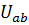 , так как в третьей ветви нет источников МДС.
, так как в третьей ветви нет источников МДС.
По первому закону Кирхгофа для узла а можно записать
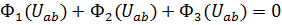
Графическое решение этого уравнения проводится сложением графиков ВАХ потоков при различных значениях магнитного напряжения 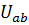 . Результатом графического сложения будет график зависимости суммарного потока от магнитного напряжения между узлами цепи
. Результатом графического сложения будет график зависимости суммарного потока от магнитного напряжения между узлами цепи 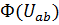 .
.
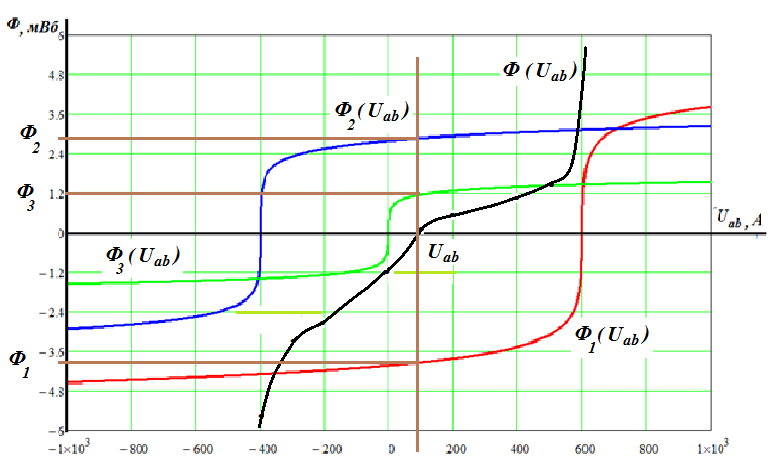
Пересечение графика суммарного потока с осью магнитного напряжения обеспечивает выполнение первого закона Кирхгофа, то есть равенство нулю. При этом магнитное напряжение 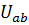 будет равно
будет равно
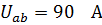
При этом напряжении магнитные потоки в ветвях магнитной цепи по графикам равны
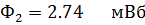
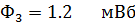
Дата добавления: 2020-03-21; просмотров: 1193;











