Дві прямі в просторі.
7.7.1. Паралельність прямих.
Дослідження взаємного розташування двох прямих в просторі вимагає комплексного застосування апарату векторної алгебри. Розглянемо випадок, коли прямі задані своїми канонічними рівняннями. Отже, нехай
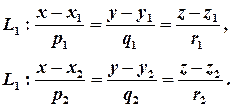
Знаменники дробів – це відповідні координати направляючих векторів прямих. Прямі паралельні тоді і тільки тоді, коли їх направляючі вектори колінеарні, звідки
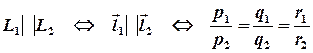 .
.
7.7.2. Умова перетину просторових прямих.
Нехай тепер прямі непаралельні. Тоді вони або мимобіжні, або перетинаються. Розглянемо малюнок

З рівнянь прямих ми отримуємо інформацію про направляючі вектори прямих та про точки, що їм належать. Оскільки вектори в аналітичній геометрії є вільними, можна вважати, що їх початки співпадають з відповідними точками. Сполучимо ці точки і утворимо вектор 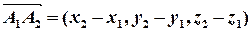 . Очевидно, що прямі перетинаються тоді і тільки тоді, коли вони лежать в одній площині (це з урахуванням того, що прямі, за припущенням, непаралельні), а отже, тоді і тільки тоді, коли вектори
. Очевидно, що прямі перетинаються тоді і тільки тоді, коли вони лежать в одній площині (це з урахуванням того, що прямі, за припущенням, непаралельні), а отже, тоді і тільки тоді, коли вектори 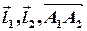 є компланарними, тобто, тоді і тільки тоді, коли їх змішаний добуток дорівнює 0, остаточно
є компланарними, тобто, тоді і тільки тоді, коли їх змішаний добуток дорівнює 0, остаточно
 .
.
7.7.3. Знаходження пари найближчих точок на мимобіжних прямих.
Нехай тепер прямі і не паралельні, і не перетинаються, тобто вони мимобіжні. Тоді виникає важливе питання про знаходження пари найближчих точок на цих прямих. Геометричні міркування доводять, що така пара точок існує, і ці точки є кінцевими точками спільного перпендикуляра до цих прямих – на малюнку це перпендикуляр PQ :

Це поки що, так би мовити, „чиста” геометрія. Переходимо до аналітичної геометрії.
З рівнянь прямих ми отримуємо інформацію про координати точок, які належать прямим, та про координати векторів, паралельних даним прямим:
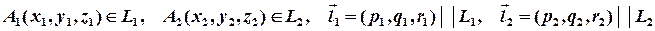 .
.
Пам’ятаємо, що вектори в аналітичній геометрії вільні (їх можна вільно переносити куди завгодно, але паралельно й зі збереженням довжини ), отже, маємо право вважати, що направляючі вектори прямих лежать на цих прямих і, більше того, виходять з точок відповідно А1 і А2:

Якщо прямі  і
і  і не паралельні, і не лежать в одній площині, то вони мимобіжні, лежать в паралельних площинах, і на кожній з них існує по одній-єдиній точці, які разом утворюють пару найближчих точок – ці точки є кінцевими точками спільного перпендикуляру до цих прямих.
і не паралельні, і не лежать в одній площині, то вони мимобіжні, лежать в паралельних площинах, і на кожній з них існує по одній-єдиній точці, які разом утворюють пару найближчих точок – ці точки є кінцевими точками спільного перпендикуляру до цих прямих.
Кожну точку з пари найближчих точок знаходимо послідовно, перекладаючи на аналітичну мову відповідні геометричні побудови.
Точка P, що належить прямій  , є точкою перетину прямих
, є точкою перетину прямих  і
і  . Пряма
. Пряма  є проекцією прямої
є проекцією прямої  на площину
на площину 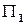 . Ця площина проходить через пряму
. Ця площина проходить через пряму 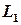 і паралельна прямій
і паралельна прямій  ; отже ця площина однозначно визначається умовами: точка
; отже ця площина однозначно визначається умовами: точка 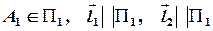 . Таким чином, за нормальний вектор
. Таким чином, за нормальний вектор 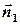 цієї площини можна взяти векторний добуток
цієї площини можна взяти векторний добуток 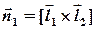 і скласти рівняння цієї площини, маючи точку і нормальний вектор. Тепер увага: нашою метою є знаходження координат точки Р, а вона є точкою перетину прямої
і скласти рівняння цієї площини, маючи точку і нормальний вектор. Тепер увага: нашою метою є знаходження координат точки Р, а вона є точкою перетину прямої 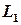 з проектуючою площиною
з проектуючою площиною  , яка проектує пряму
, яка проектує пряму  на площину
на площину 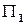 :
:

Ця проектуюча площина  проходить через пряму
проходить через пряму  , а отже вона містить точку
, а отже вона містить точку  і направляючий вектор
і направляючий вектор 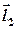 паралельний цій площині. Оскільки
паралельний цій площині. Оскільки  є проектуючою площиною, то вона є перпендикулярною до площини
є проектуючою площиною, то вона є перпендикулярною до площини 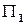 , а отже нормальний вектор площини
, а отже нормальний вектор площини 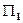 має бути паралельним площині
має бути паралельним площині  . Таким чином, проектуюча площина
. Таким чином, проектуюча площина 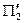 визначається такою інформацією:
визначається такою інформацією:
 .
.
Ми знову приходимо до можливості скласти рівняння площини  , маючи точку і нормальний вектор, а саме:
, маючи точку і нормальний вектор, а саме:  і
і 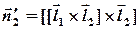 . Приходимо до задачі знаходження точки перетину прямої і площини, розглянутої в §2.
. Приходимо до задачі знаходження точки перетину прямої і площини, розглянутої в §2.
Точку Q знаходимо аналогічними, точніше сказати, двоїстими, міркуваннями.
Вправа. Побудувати схему знаходження точки 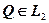 .
.
Приклад. З’ясуємо взаємне розташування прямих
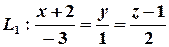 ,
,
 .
.
Очевидно, що прямі 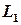 і
і  не паралельні. З’ясуємо, чи не є вони компланарні (а отже, чи не перетинаються вони):
не паралельні. З’ясуємо, чи не є вони компланарні (а отже, чи не перетинаються вони):
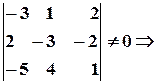 не перетинаються.
не перетинаються.
Отже, прямі мимобіжні, і існує пара найближчих точок на цих прямих. Для знаходження однієї з цих точок,  , складаємо рівняння площини
, складаємо рівняння площини 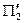 , для чого спочатку знаходимо
, для чого спочатку знаходимо
 .
.
Тепер обчислюємо
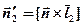
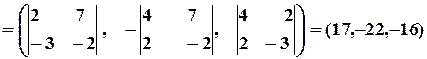 .
.
Для знаходження однієї з пари найближчих точок – точки Р – треба розв’язати СЛР:
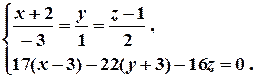
Вправа. Завершити розв’язання задачі знаходження пари найближчих точок на прямих L1 і L2 .
Дата добавления: 2021-05-28; просмотров: 587;











