Знаходження точки перетину двох прямих ліній на площині.
Нехай маємо дві прямі лінії, які задані рівняннями:
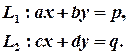
Припустимо, що ці прямі не паралельні. В §1встановлено, що умовою паралельності прямих є пропорційність відповідних коефіцієнтів при змінних. Отже, нехай коефіцієнти не пропорційні. Тоді ці прямі неодмінно мають точку перетину, і до того ж тільки одну. Це, так би мовити, принципова геометрична інформація. Далі виконуємо аналітичну роботу: знаходимо координати точки перетину. Для цього треба розв’язати СЛР:
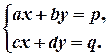
Якщо перше рівняння помножити на 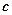 , друге помножити на
, друге помножити на 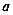 і від першого відняти друге, у формальному запису
і від першого відняти друге, у формальному запису
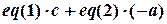 ,
,
то коефіцієнт при 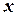 буде рівний 0, тобто змінна
буде рівний 0, тобто змінна 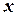 буде виключена, утвориться рівняння від однієї змінної
буде виключена, утвориться рівняння від однієї змінної 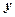 :
:
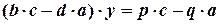 ,
,
звідки
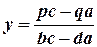 .
.
Виключивши подібним чином змінну 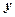 (пояснити, як саме: вказати відповідне перетворення), отримаємо:
(пояснити, як саме: вказати відповідне перетворення), отримаємо:
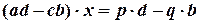 ,
,
звідки
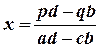 .
.
Придивимось уважно до отриманих формул, які визначають значення координати точки перетину. Ми побачимо, що вирази у чисельниках і знаменниках утворені за однаковою алгебраїчною схемою:
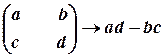 ,
,
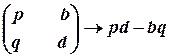 ,
,
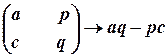 .
.
Таблиця
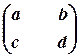
називається матрицею розмірів 2х2 (або квадратною матрицею порядку 2), а число, обчислене за правилом: ліве верхнє число помножити на праве нижнє число мінус праве верхнє число помножити на ліве нижнє число, – називається визначником (або детермінантом) цієї матриці, точніше, визначником другого порядку. Відповідний вираз – він же є визначник – має своє позначення:
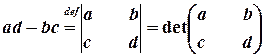 .
.
Таким чином, маємо формули:
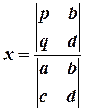 ,
, 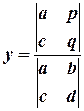 .
.
Стосовно розглядуваної задачі знаходження розв’язку СЛР використовується спеціальна термінологія і позначення:
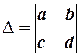 – основний визначник (складений з коефіцієнтів при змінних);
– основний визначник (складений з коефіцієнтів при змінних);
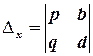 – допоміжний визначник– чисельник дробу для обчислення
– допоміжний визначник– чисельник дробу для обчислення 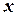 ;
;
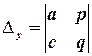 – допоміжний визначник – чисельник дробу для обчислення
– допоміжний визначник – чисельник дробу для обчислення 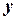 .
.
Таким чином, доведена
Теорема Крамера для СЛР 2х2. Якщо основний визначник 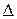 СЛР
СЛР
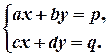
відмінний від нуля, то СЛР має, і до того ж єдиний, розв’язок, який знаходиться за формулами (правилом) Крамера:
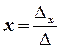 ,
, 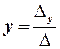 .
.
Приклад. Знайдемо точку перетину двох прямих 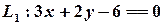 і
і 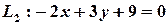 . Задача зводиться до розв’язання СЛР
. Задача зводиться до розв’язання СЛР
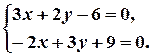
Увага: формули Крамера виведені для такого запису СЛР, у якому вільні члени знаходяться в правих частинах СЛР. Виконаємо потрібне перетворення:
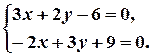
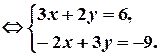
Тепер усе готове до застосування правила Крамера.
Порада: для людей з не дуже великим практичним математичним досвідом дуже корисним буде супроводжувати аналітичні перетворення геометричними ескізами. От, наприклад, попереднє зауваження. Раптом людина забула перенести у рівняннях прямих вільні члени у праві частини (автор багато-багато разів спостерігав це явище), – тоді (при подальших правильних діях) вона отримає числа, протилежні за знаком істинним координатам точки перетину прямих. Навіть нашвидкуруч виконаний малюнок застереже від принципової помилки:
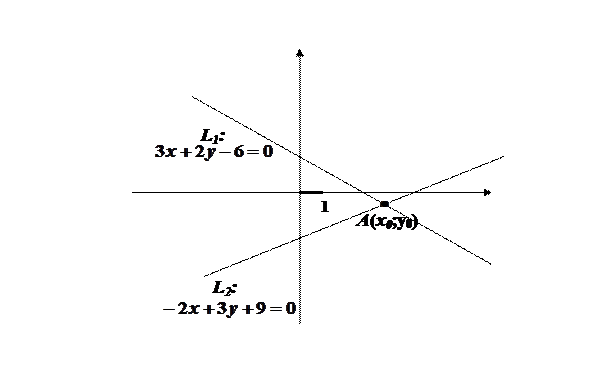
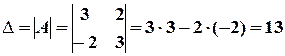 ≠ 0 (не важливо, додатнє значення має визначник чи від’ємне, аби не нульове)
≠ 0 (не важливо, додатнє значення має визначник чи від’ємне, аби не нульове)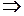 правило Крамера можна застосовувати.
правило Крамера можна застосовувати.

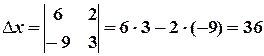 ,
,
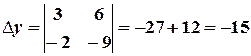 ,
,
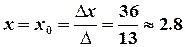 ,
, 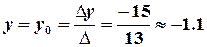 .
.
Знайдені значення координат точки перетину прямих не протирічать малюнку. Робимо аналітичну перевірку:
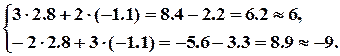
Остаточно: точка перетину прямих 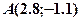 .
.
Дата добавления: 2021-05-28; просмотров: 673;











