Декартова система координат. Координати точки.

Метод координат і є тим „містком”, який сполучає фігури і числа, тобто реалізує ідею за числами бачити фігури, а за фігурами числа.

Найпростіша геометрична фігура – точка – нескінченно мала „цеглинка”, з яких побудовані всі інші фігури. Евклід дав такі означення: точка – це те, частина чого є ніщо, лінія – це довжина без ширини. „Означення” Евкліда – не є означеннями в строгому розумінні, це лише образи, породжені нашими відчуттями. Аналітична геометрія звужує множину невизначених первісних понять і саме за допомогою методу координат.

Точка – найпростіше геометричне поняття. Число – найпростіше арифметичне (алгебраїчне, аналітичне) поняття. За „стратегічною” ідеєю аналітичної геометрії треба точці – геометричному поняттю – поставити у відповідність „щось” арифметичне.

Розв’язання задачі про визначення місця для побудови збагачувальної фабрики між двома шахтами (див. вступ) здійснене саме з використанням методу координат. Воно починається з малюнка і слів:

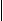
0 90

АВ

Позначимо шахти точкамиАіВначисловій прямій.

Означення (числової прямої (або числової осі)).Числовою прямою називається пряма, кожна точка якої ототожнена з дійсним числом: вибрано початкову точку О (початок координат) – число 0 , один вважається додатнім, відрізок , що є одиницею виміру довжин — масштаб.

Кожному дійсному числу ставиться у відповідність одна і тільки одна точка числової прямої за таким правилом:

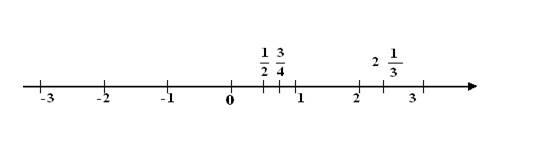
числу 0 відповідає точка O, яка називається початком координат; кожному числу 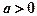відповідає точка A, яка лежить на відстані праворуч від початкової точки O; кожному числу 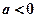відповідає точка A, яка лежить на відстані 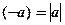ліворуч від початкової точки O ( віддаль вимірюється вибраним масштабом). Число a називається координатою точки A, позначається A(a). Отже, усім дійсним числам відповідають точки числової прямої.

Означення (декартової системи координат). Дві взаємно перпендикулярні числові осі Ox і Oy, що мають спільний початок O та мають певне узгодження за напрямком, називають декартовою прямокутною системою координат на площині з початком координат в точці O та осями координат - віссю абсцис Ox та віссю ординат Oy ; площину на якій задана система координат, називають координатною площиною.

На практиці найчастіше використовують координатні осі з рівними масштабними відрізками, але це не є обов’язковою вимогою.

Нехай M - довільна точка координатної площини. Спроектуємо ортогонально точку М на осі Oxі Oy. Відповідні проекції (точки) позначимо M_x і M_y . Ці проекції є точками числових осей, отже їх можна ототожнити з певними числами х (абсциса) і у (ордината).

Означення (координат точки). Числа x, y (записані у вказаному порядку), що є проекціями точки М на координатні осі, називають координатами точкиM ; при цьому пишутьM(x, y).

Отже, кожній точці площини ставиться у відповідність впорядкована пара дійсних чисел (x, y)- декартових прямокутних координат цієї точки. У свою чергу, кожна впорядкована пара дійсних чисел (x, y) визначає єдину точкуM, для якої x є абсцисою, а y- ординатою. Таким чином, введення на площині прямокутної декартової системи координат встановлює взаємно однозначну відповідність між точками площини і впорядкованими парами дійсних чисел.

Цілком аналогічно вводиться поняття декартової системи координат в просторі і координат просторової точки:

Означення (Декартової системи координат в просторі). Декартовою системою координат в просторі називається трійка взаємно перпендикулярних числових осей, точка перетину яких є нулем кожної з осей і додатні напрямки вибрані так, щоб система координат була правильною:

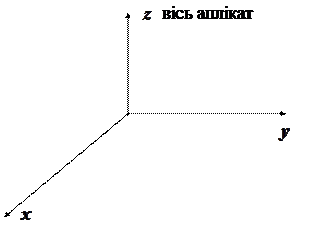Якщо на площині або в просторі введена декартова система координат, тоді площина і простір звуться координатними, і тоді кожній точці взаємно однозначно відповідають пара чисел для площини і трійка чисел для простору, які однозначно визначають положення точки. Можна сказати, що координати точки – це її „адреса” на площині або в просторі.