Анализ технологического объекта управления

Задачи анализа технологического объекта управления решаются с использованием временных и частотных характеристик, которые средствами MatLab автоматически рассчитываются с помощью следующих команд:

- переходная характеристика дискретной модели >> step(Wz);

- переходная характеристика непрерывной модели >> step(Ws);

- импульсная характеристика дискретной модели >> impulse(Wz);

- импульсная характеристика непрерывной модели >> impulse(Ws);

- частотные характеристики ЛАХ и ЛФХ дискретной модели
>> bode(Wz);

- частотные характеристики ЛАХ и ЛФХ непрерывной модели
>> bode(Ws);

- амлитудно-фазовые частотные характеристики дискретной (АФЧХ) модели >> nyquist(Wz);

- амлитудно-фазовые частотные характеристики непрерывной (АФЧХ) модели >> nyquist(Ws).

Результаты построения временных и частотных характеристик исследуемой непрерывной модели показаны на рис. 19, 20 и 21.

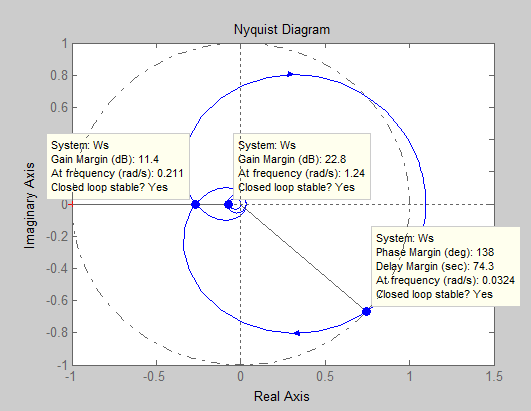
Рисунок 19 – Амплитудно-фазовая частотная характеристика непрерывной (АФЧХ) модели

Для оценки работоспособности системы автоматического управления воспользуемся критерием Найквиста, согласно которому АФЧХ разомкнутой САУ не должна на комплексной плоскости охватывать точку с координатами
(-1, j0) при изменении частоты в пределах 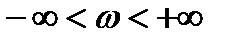[9].

В соответствии с полученной диаграммой на рис. 19 для исследуемого технологического объекта можно сделать вывод об ее устойчивости по критерию Найквиста.

Для того чтобы построить график переходного процесса воспользуемся функцией >> step(Ws), результаты работы которой показаны на рис. 20.

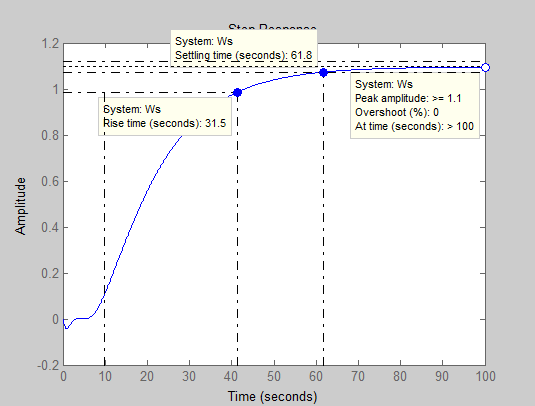
Рисунок 20 – Переходная характеристика непрерывной модели

В соответствии с полученным графиком переходного процесса (рис. 20) оценим значения основных показателей качества системы автоматического управления технологическим объектом:

- время нарастания (Rise time) – 31,5 с;

- время переходного процесса (Setting time) – 61,8 с;

- установившееся значение выходной величины (Final value) – 1,1;

- пиковая амплитуда (Peak amplitude) – 1,1;

- перерегулирование (Overshoot) – 0%;

- статическая ошибка – 10%.

Частотные характеристики (рис. 21) исследуемой непрерывной САУ системы получим, используя встроенную функцию >> bode(Ws). Дополнительными показателями качества работы системы в установившемся режиме являются запасы устойчивости.

Запасом устойчивости по амплитуде называют величину 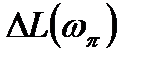, на которую нужно изменить коэффициент преобразования системы для того, чтобы привести её к границе устойчивости, т.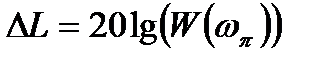е. , где 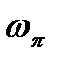– частота, при которой фазовая характеристика равна -p.

Запасом устойчивости по фазе называют угол 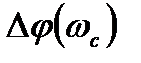, на который фазовая характеристика разомкнутой системы на частоте среза 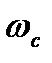(когда 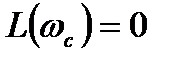) отличается от угла ±180°, т.е. .

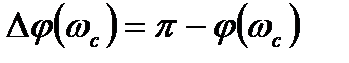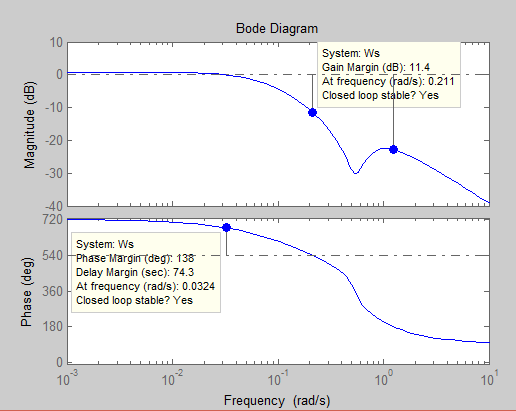
Рисунок 21 – Частотные характеристики (ЛАХ и ЛФХ) непрерывной модели

По графикам частотных характеристик ЛАХ и ЛФХ (рис. 21) разомкнутой САУ оценим значения запасов устойчивости:

- по амплитуде (Gain Margin) для непрерывной модели – 11,4 дБ ;

- по фазе (Phase Margin) для непрерывной модели - 138°.

Значения запасов устойчивости можно определить также и в режиме командной строки MATLAB с помощью команд:

>> [Gm,Pm,Wcg,Wcp]=margin(Wz) – для дискретной модели:

>> [Gm,Pm,Wcg,Wcp]=margin(Ws) – для непрерывной модели:

где Gm – запас устойчивости по амплитуде в натуральных величинах на частоте Wcg; Pm – запас устойчивости по фазе на частоте Wcp.

Для определения запасов устойчивости в логарифмическом масштабе применяется команды:

>> Gmlog=20*log10(Gm)– для дискретной модели:

>> Gmlog=20*log10(Gm) – для непрерывной модели.

При решении задач управления методами теории пространства состояний предварительно рассматриваются фундаментальные свойства динамических систем, которые не встречаются в классической теории управления, оперирующей только входными и выходными сигналами элементов рассматриваемой системы. Такими свойствами являются управляемость и наблюдаемость.

Теоретическая справка [10-13]:

Рассмотрим n-мерное пространство состояний , в котором каждому состоянию соответствует некоторое положение изображающей точки, определяемое значениями переменных состояния .

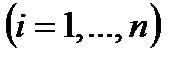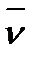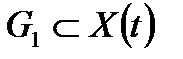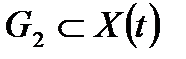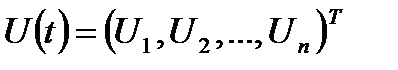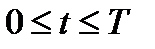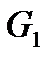Пусть в пространстве состояний заданы два множества и . Рассматриваемая система будет управляемой, если существует такое управление , определенное на конечном интервале времени , которое переводит изображающую точку в пространстве из подобласти в подобласть .

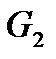Следует отметить, что признак управляемости применим не только к динамическим объектам, но и к системам, содержащим множество замкнутых контуров управления. Управляемость зависит от структуры системы, состава органов управления и значений параметров.

Проведем анализ специфических свойств объектов управления, представленных векторно-матричными моделями в непрерывном времени

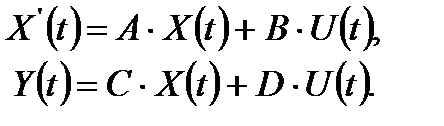(7)

где – вектор фазовых координат или состояний исследуемого объекта, – вектор управляемых (выходных) величин системы, 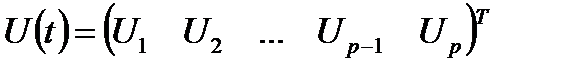– вектор управляющих (входных) воздействий, А – матрица коэффициентов размерности 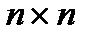, В – матрица коэффициентов размерности ,
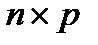С – матрица управления размерности 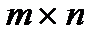, D – сквозная матрица размерности .

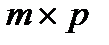Р. Калман показал, что линейная стационарная система будет полностью управляемой, если ранг матрицы управляемости и порядок системы совпадают:

,

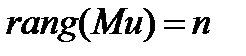где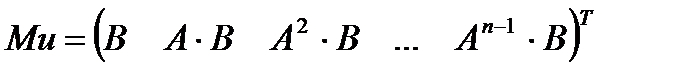

Система считается наблюдаемой, если в формировании вектора выходных координат участвуют все составляющие вектора переменных состояния . Таким образом, если на конечном интервале времени по выходу системы в конце этого интервала можно определить все начальные компоненты вектора состояния при известном управляющем воздействии, то система будет наблюдаемой.

Р. Калман доказал, что линейная стационарная система является полностью наблюдаемой, если ранг матрицы наблюдаемости равен порядку исследуемой системы:

,

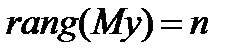где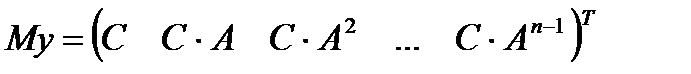

Воспользуемся встроенной в пакет Control System Toolbox функцией ctrb(А,В), чтобы сформировать матрицу управляемости в пространстве состояний. Для этого необходимо вычислить матрицы A, B, C, D с помощью команд:

>> [A,B,C,D]=ssdata(Ws)

A =

B =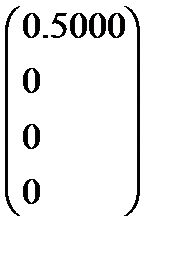

C =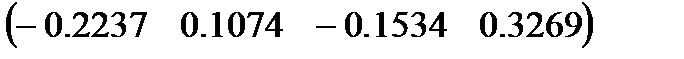

D =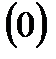

>> Mu=ctrb(A,B)

Mu=

>> n1=rank(Mu)

n1=4

Таким образом, для исследуемой модели объекта размерность вектора состояний, определяемая размером матриц A и B равна четырем и ранг матрицы управляемости Mu также равен четырем, следовательно рассматриваемый технологический объект управления является полностью управляемым.

Рассчитаем матрицу наблюдаемости, используя встроенные команды MatLab:

>>My=obsv(A, C)

My =

>> n2=rank(My)

n2=4

Для исследуемой модели ранг матриц наблюдаемости и матриц А и С для рассматриваемого технологического объекта управления также совпадают, следовательно, объект автоматизации является полностью наблюдаемым, т.е. для всех значений выходной величины Y(t) может быть определен вектор переменных состояния X(t), необходимый для синтеза системы управления.