Глава 2. Синтез регулятора системы автоматического управления
Проблема выбора структуры и синтеза настроек регуляторов является наиболее сложной в теории и технике построения сложных систем автоматического управления [15]. В работах А. М. Летова, Р. Калмана впервые была поставлена, а затем в работах А.А. Красовского, М.М. Атанса и П.Фабла получила развитие теория аналитического конструирования оптимальных регуляторов. Аналитический обзор работ, посвященных оптимальному управлению динамическими объектами, приведен в журнале «Автоматика и телемеханика» [16]. Согласно определению А.М. Летова синтез закона управления представляет собой функцию координат состояния объекта, полученную на основе математического анализа, исходя из единых требований к качеству переходного процесса в форме минимуму оптимизирующего функционала [9, 15, 17 – 21].
В работах [21, 22] А. А. Колесникова предлагается перейти от переменных в пространстве состояний к управлению агрегатными макропеременными в виде функций фазовых координат и параметров обратных связей. Численный метод структурно-параметрического синтеза регулятора, описанный в работах [20, 24], основан на построении множества функциональных зависимостей управления от координат пространства состояний и поиске оптимального решения с помощью генетического алгоритма. Отличительной особенностью подхода от задач вариационного оптимального управления является учет в постановке задачи всех свойств синтезированного управления.
Оптимизация, основанная на ЛПt - последовательности [25-27] позволяет решать задачи поиска оптимальных как параметров и режимов работы, так и синтеза систем управления. Адаптивный метод исследования пространства параметров, в основе которого лежит корректное определение допустимого множества решений использует в процессе поиска решения необходимые и достаточные условия оптимальности, что обеспечивает равномерное зондирование пространства параметров, учет множества критериев и принятие решения из множества Парета.
Под устойчивостью системы автоматического управления с ПИД-регулятором понимается способность системы возвращаться к слежению за уставкой после прекращения внешних воздействий. При этом под внешними воздействиями следует понимать не только любые возмущения, действующие на объект, но и шумы измерений, нестабильность уставки, шумы дискретизации и квантования и т.д. В производственных условиях попытки добиться устойчивости экспериментальным путем без идентификации объекта управления невозможно, поэтому практический интерес представляет анализ запасов устойчивости:
· запас по усилению – величина, на которую необходимо умножить передаточную функцию разомкнутой системы (состоящей из контроллера R(p) и объекта управления W(p)), чтобы ее модуль на частоте сдвига фаз 180° стал равен 1:
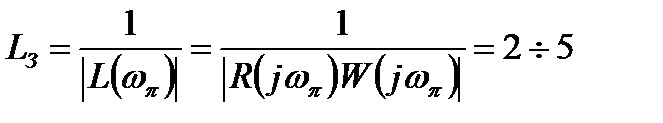 .
.
· запас по фазе (минимальная величина 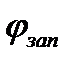 , на которую необходимо увеличить фазовый сдвиг в разомкнутой системе, чтобы суммарный фазовый сдвиг достиг 180°):
, на которую необходимо увеличить фазовый сдвиг в разомкнутой системе, чтобы суммарный фазовый сдвиг достиг 180°):
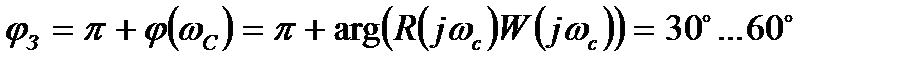 .
.
· запас устойчивости – минимальное расстояние от кривой годографа частотной передаточной функции до точки 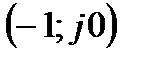 :
:
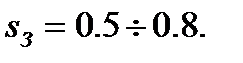
· запас по задержке – минимальная задержка, при добавлении которой контур не теряет устойчивость. Используется в случае, если годограф АФЧХ несколько раз пересекает ось действительных чисел. Для характеристики запасов выбирают точку наиболее близко расположенную к 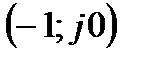
Для приведения переходного процесса к оптимальному виду следует руководствоваться правилами:
· увеличение значения пропорционального канала регулирования приводит к увеличению быстродействия системы, но снижает запас устойчивости;
· уменьшение интегральной составляющей регулятора приводит к ускорению процесса ликвидации ошибки регулирования, а также сокращению запаса устойчивости;
· увеличение дифференциального канала регулирования увеличивает запас устойчивости и быстродействие системы.
Недостатком всех экспериментальных методик настройки регуляторов является неполнота информации о запасе устойчивости (с помощью критериев, позволяющих судить о том, как далеко находится система от состояния неустойчивости) и робастности системы, что является особенно актуальным для обеспечения надежности работы регулятора и всей системы в целом.
Высокая чувствительность САУ с ПИД-регулятором к отклонению от оптимальных значений каналов требует обоснованного выбора критерия точности регулирования и надежности ПИД-регулятора.
В нефтехимическом производстве приняты следующие критерии качества переходного процесса [8]:
· динамическая ошибка, значение которой не должно превышать заданной величины:
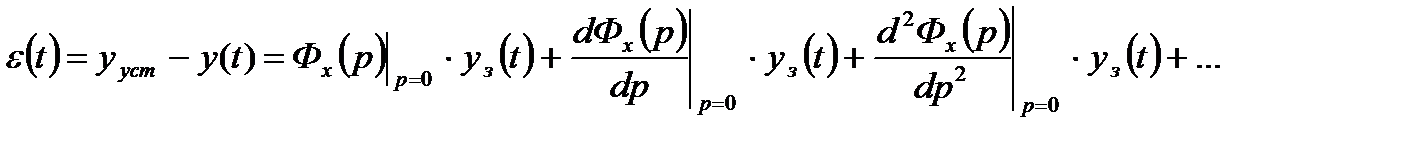 ,
,
где 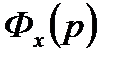 – передаточная функция по ошибке.
– передаточная функция по ошибке.
· Колебательность не должна превышать значения для нефтехимических технологических процессов (1,1¸1,5) % для обеспечения монотонных апериодических переходных процессов в системе:
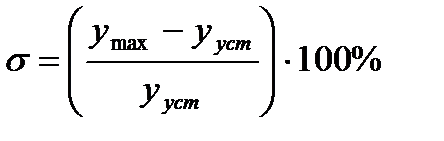
· площадь под кривой разгона или вторая интегральная оценка должна быть минимальна при условии 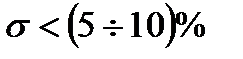 :
:
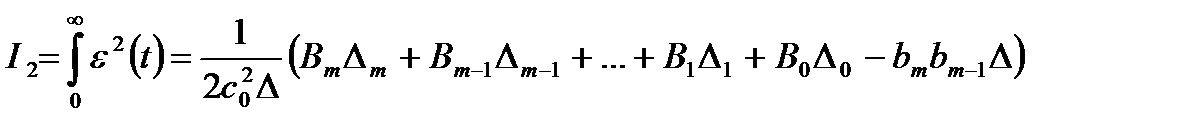 ,
,
где 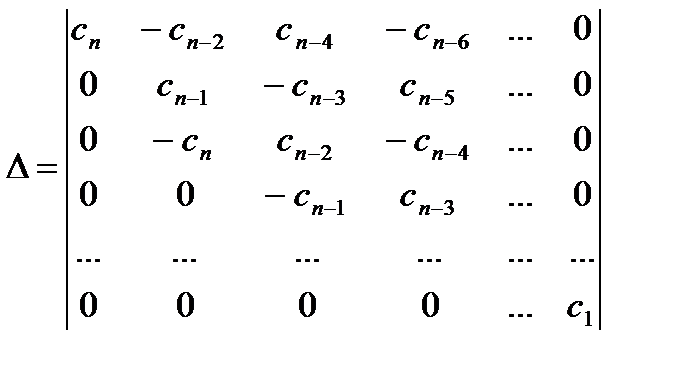 - матрица, составленная из коэффициентов при производных от выходной величины
- матрица, составленная из коэффициентов при производных от выходной величины 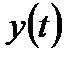 :
:
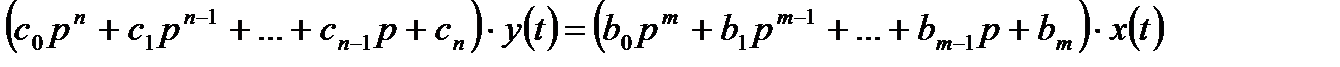 .
.
Определители 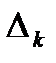 получаются из исходной матрицы
получаются из исходной матрицы  путем замены столбца с номером
путем замены столбца с номером 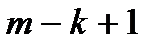 на матрицу столбец
на матрицу столбец 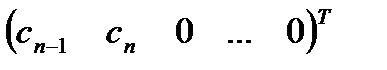 для
для 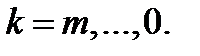
Коэффициенты 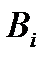 при производных от входного сигнала определяются по формулам:
при производных от входного сигнала определяются по формулам:
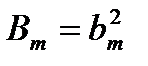 ,
, 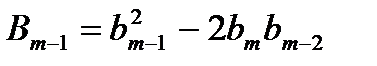 ,
, 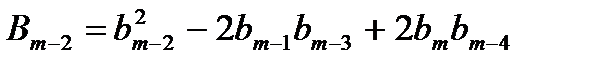 , …,
, …, 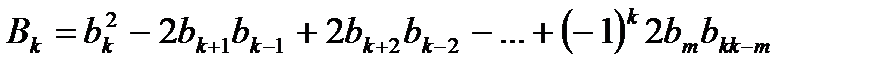 , …,
, …, 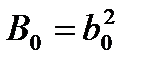 .
.
Приведенные формулы применимы, если выполняется условие 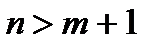 .
.
Интегральный критерий 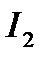 прямо пропорционален интегральной составляющей
прямо пропорционален интегральной составляющей 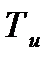 регулятора и обратно пропорционален пропорциональной
регулятора и обратно пропорционален пропорциональной 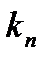 , увеличение последней (
, увеличение последней ( 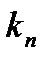 ) для постоянного значения составляющей дифференциального канала
) для постоянного значения составляющей дифференциального канала 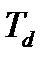 соответствует уменьшению
соответствует уменьшению 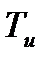 .
.
Дата добавления: 2021-05-28; просмотров: 679;











