Каноническое распределение Гиббса.

Пусть теперь интересующая нас система незамкнута, не изолирована, и возможен теплообмен с окружающей средой, то есть система 1 составляет малую, но макроскопическую часть системы 2, так что N₁>>1, N₂>>1, N₂>>N₁. Предположим также, что обмена частицами нет, оболочка непроницаема, но обмен энергией возможен. Как мы уже выяснили 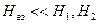и полная энергия системы:

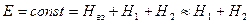(система 1+2 – изолирована) (20)

Тогда для системы 1+2 справедливо распределение (18):

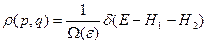(21) – это плотность вероятности обнаружить систему 1 в состоянии Г₁(q₁, p₁), а систему 2 – в состоянии Г₂(q₂, p₂) или при условии, что 2 в состоянии (q₂, p₂). Но нас не интересует система 2, мы только знаем, что она есть, и для того, чтобы найти 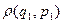, мы должны проинтегрировать (21) по dГ₂=dq₂dp₂:

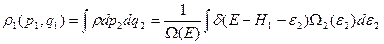
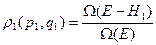(22)

Из (22) видно, что поскольку (например) для идеального газа Ω₂ растёт с (E-H₁), то ρ₁ должно убывать с ростом H₁ – своей энергии. Для дальнейшего вывода ограничимся (по-прежнему), систему 2 возьмём идеальным газом – чтобы избежать излишних математических сложностей. Тогда:

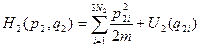(23)

Тогда:

*

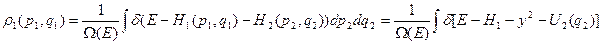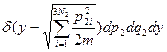* (24)

В (24) искусственно ввели δ функцию от y. Действительно, проинтегрировав по y – получим правильный ответ. Теперь, однако, изменяем порядок интегрирования и проведём его по dp₂:

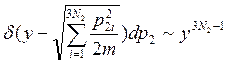
Почему? δ функция выделяет интеграл по одной из переменных p_2j (j=1, например, dp₂= dp₂₁… dp_2N2)

p₂ max равно (см. подкоренное выражение) 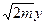- радиус 3N₂-мерной сферы, мы вычислили её «площадь». Тогда продолжим 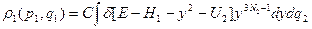(24):

(24’)

Далее интегрируем с учётом δ функции:

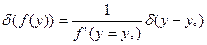, где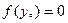

В результате имеем:

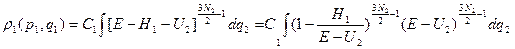(24’’)

При 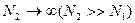величина H₁ мала, и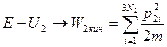

Введём такой параметр:

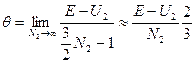(25)

Видно, что θ имеет порядок средней кинетической энергии, приходящейся на одну частицу термостата. Тогда для первого сомножителя под интегралом имеем:

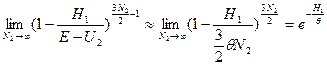
Второй множитель под интегралом от q₂ не зависит, и интегрирование по dq₂ даёт константу.

В итоге имеем для распределения системы, находящей в термостате:

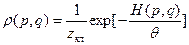(26) – каноническое распределение Гиббса

θ – модуль распределения, а постоянная z_кл определяется из условия нормировки

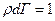
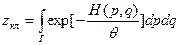(27)

z_кл – классический статический интеграл.

z_кл зависит от параметров нашей системы 1 (от Н), а θ определяется только средней кинетической энергией частиц в термостате!!!

Если разделим нашу систему 1 на две макроскопические части 1₁ и 1₂, взаимодействующие с одним термостатом (θ), то Н₁=Н₁₁+Н₁₂.

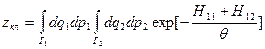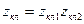→ и 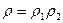- мультипликативность канонического распределения (следовало ожидать для слабо взаимодействующих систем).

Другая запись (26):

Обозначим

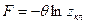(28)

Тогда (26):

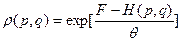(29)

В дальнейшем увидим, что F имеет смысл введённой ранее свободной энергии, а θ – абсолютной температуры.