О статичстическом смысле термодинамических величин. Обоснование I-го и II-го начал термодинамики.
Если рассматриваемая нами система неподвижна как целое, то гамильтониан H(p,q,xi) – совпадает с полной энергии системы. Её можно назвать микроскопической внутренней энергией системы. Что же такое U(T,xi) (термодинамическая внутренняя энергия)?
Согласно (6), её можно определить следующим образом:
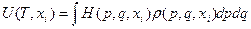 (31)
(31)
- среднее значение внутренней энергии H. Отметим, что функция U = U(T,xi) называется в ряде случаев калорическим уравнением состояния. (например, для идеального газа U = cVT, для газа Ван-дер-Ваальса: U = cVT – а/V.
Рассмотрим теперь уравнение (I) – I начало термодинамики:
đQ* = dU + dA (I)
где U – функция состояния, dU – полный дифференциал, и
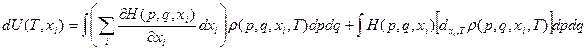 (32)
(32)
Здесь 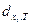 - дифференциал в системе переменных T,xi -
- дифференциал в системе переменных T,xi - 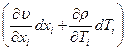 (xi – внешние переменные).
(xi – внешние переменные).
Примечание: U – функция состояния, зависит от внешних параметров и от температуры Т (вспоминаем основной принцип – зависимость от внешних параметров и температуры).
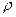 - зависит от энергии и, естественно также, от внешних параметров. Следовательно, от температуры Т и от внешних параметров также. (T – термодинамическая абсолютная температура). Но вообще говоря,
- зависит от энергии и, естественно также, от внешних параметров. Следовательно, от температуры Т и от внешних параметров также. (T – термодинамическая абсолютная температура). Но вообще говоря, 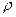 в выводе распределения Гиббса не зависит от температуры, а зависит от от
в выводе распределения Гиббса не зависит от температуры, а зависит от от 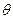 – модуля распределения (средней кинетической энергии). Мы уже сейчас можем предположить, что температура и средняя кинетическая энергия связаны между собой и практически представляют собой одно и тоже. Но пока подождём с выводами. По чистой математике, пусть пока U тоже зависит от
– модуля распределения (средней кинетической энергии). Мы уже сейчас можем предположить, что температура и средняя кинетическая энергия связаны между собой и практически представляют собой одно и тоже. Но пока подождём с выводами. По чистой математике, пусть пока U тоже зависит от 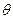 .
.
Из (32) видно, что можно ввести микроскопические силы (зависящие от p и q) – FiM, соответствующие некоторым обобщённым координатам xi – внешним параметрам:
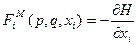
при этом наши обобщённые термодинамические силы, которые вводили при рассмотрении I начала термодинамики – Xi, определяются как
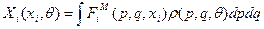 (33)
(33)
- среднее от микроскопических сил. Но 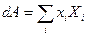 (из термодинамики). Видно, что первый член в правой части (32) равен работе термодинамических сил, и, с учётом (33), (32) тогда можем переписать в виде:
(из термодинамики). Видно, что первый член в правой части (32) равен работе термодинамических сил, и, с учётом (33), (32) тогда можем переписать в виде:
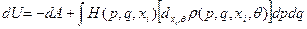 (34)
(34)
Сравнивая теперь (I) и (34), находим статистическое определение đQ*:
đQ* = 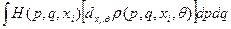 (35)
(35)
- та часть изменения внутренней энергии, которая определяется не работой, а изменением функции распределения 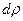 вследствие изменения термодинамических переменных xi,
вследствие изменения термодинамических переменных xi, 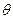 (
( 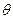 - средняя кинетическая энергия, можем считать термодинамической переменной).
- средняя кинетическая энергия, можем считать термодинамической переменной).
Перейдём к рассмотрению II-го начала термодинамики:
Покажем сначала (с помощью математических уравнений, что, используя конкретный вид распределения Гиббса (29), можно представить выражение (35) в виде II: (II: đQ* = TdS) и 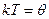 .
.
Для этого нам понадобятся два равенства:
(а) 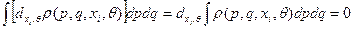 - следствие условие нормировки;
- следствие условие нормировки;
(б) 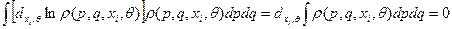
 - очевидно.
- очевидно.
Теперь (35)* 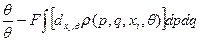
В результате имеем:
đQ* = 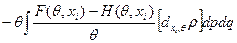 ,
,
используя распределение Гиббса в виде (29), это равенство можно переписать в следующем виде:
đQ* = 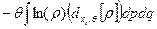 ,
,
И наконец, используя (б),
đQ* = 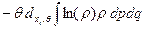 (36)
(36)
Таким образом, đQ*/ 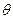 - полны дифференциал, а
- полны дифференциал, а 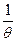 - интегрирующий множитель для đQ*. Если, таким образом, приравнять
- интегрирующий множитель для đQ*. Если, таким образом, приравнять 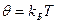 (где Т – абсолютная термодинамическая температура, kБ -размерная константа, перевод единиц измерения температуры в энергетические):
(где Т – абсолютная термодинамическая температура, kБ -размерная константа, перевод единиц измерения температуры в энергетические):
kБ = 1.38 10-16 эрг/град = 1.38 10-16 Дж/град – постоянная Больцмана. (37)
и привести (36) к виду (II): đQ* = TdS то получим следующее определение энтропии через статистическую функцию распределения:
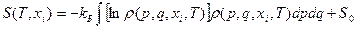 (38)
(38)
(S0 = const ). (38) можно представить в виде:
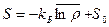 (39)
(39)
(среднее по ансамблю);
Теперь, вспомним формулу (8) с лекции 2: F = U – TS, где F – свободная энергия. Подставим в эту формулу U и S из (31) и (38), имеем:
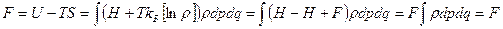
, таким образом F в (28), (29) совпадает со свободной энергией.
Отметим, что из выражения (38) для энтропии и мультипликативности распределения Гиббса для квазинезависимых подсистем в одном термостате следует аддитивность энтропии. Действительно ( 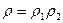 ):
):
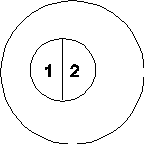
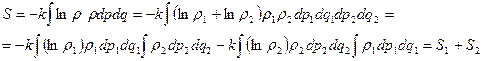
(правда следует добавить ещё +2S0, но потом покажем, что S0 = 0).
При выводе соответствия свободной энергии и энтропии мы, однако, допустили некоторую неточность.
Согласно (28) 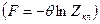 , Zкл должно быть величиной безразмерной, и согласно (38) (это видно из (б)),
, Zкл должно быть величиной безразмерной, и согласно (38) (это видно из (б)), 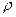 - должно быть безразмерно. Но в выражениях (26) и (27) – распределения Гиббса – это не так. Например, для системы из N взаимодействующих материальных точек Z имеет размерность
- должно быть безразмерно. Но в выражениях (26) и (27) – распределения Гиббса – это не так. Например, для системы из N взаимодействующих материальных точек Z имеет размерность 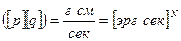 , а
, а 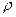 , естественно, - обратную. Хорошо бы обезразмерить, чтобы можно было брать логарифм честно. Как? Ввести новые координаты и импульсы (безразмерные) Как? Для этого следует поделить dqdp на некоторую константу, имеющую размерность [эрг*сек]. Что это за константа? Постоянная Планка:
, естественно, - обратную. Хорошо бы обезразмерить, чтобы можно было брать логарифм честно. Как? Ввести новые координаты и импульсы (безразмерные) Как? Для этого следует поделить dqdp на некоторую константу, имеющую размерность [эрг*сек]. Что это за константа? Постоянная Планка: 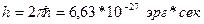 . Замена dqidpi →
. Замена dqidpi → 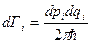 , а
, а 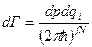 , где f = 3 – число степеней свободы в системе, а N - число частиц,
, где f = 3 – число степеней свободы в системе, а N - число частиц,
Почему бралась именно постоянная Планк и так считалась размерность? На этот вопрос можно ответить, если рассмотреть другое статистическое определение энтропии. Вспомним, что распределение по энергии 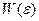 - функция достаточно острая, (это можно показать, посчитав дисперсию по
- функция достаточно острая, (это можно показать, посчитав дисперсию по 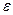 ), причём
), причём 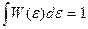 .
.
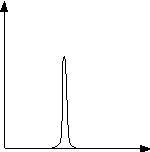
Воспользуемся простой прямоугольной аппроксимацией: 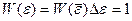 (
( 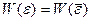 при
при 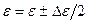 , и
, и 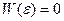 - вне интервала).
- вне интервала).
Иначе 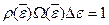 , или
, или
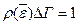 (40)
(40)
где 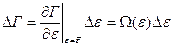
С точки зрения классической физики, макроскопическая система может находиться в любой точке фазового пространства, и число микросостояний (любые значения pi и qi) системы бесконечно велико. Однако, из квантовой механики нам известно, что существует принцип неопределённостей Гейзенберга:
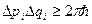
Поэтому, число микросостояний системы в объёме  равно фазовому объёму
равно фазовому объёму 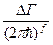 ,
, 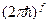 - предельный объём, элементарной ячейки, в которой может находиться частица, меньше места она занимать просто не может, и
- предельный объём, элементарной ячейки, в которой может находиться частица, меньше места она занимать просто не может, и 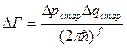 (было -
(было - 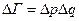 ). (Естественно, эту формулу можно обосновать и более строго из условий квантования Бора-Зоммерфельда). Но! В классической статистике константа может быть любой, только квантовая механика даёт ответ:
). (Естественно, эту формулу можно обосновать и более строго из условий квантования Бора-Зоммерфельда). Но! В классической статистике константа может быть любой, только квантовая механика даёт ответ:
Формула(26) теперь:
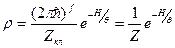
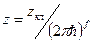
Теперь рассмотрим функцию
 (41)
(41)
Тогда с учётом (40)
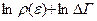 →
→ 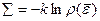 =(поскольку
=(поскольку 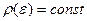 на участке
на участке 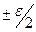 ) =
) =
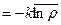 или
или 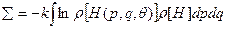 . Сравнив это с (39), получаем, что
. Сравнив это с (39), получаем, что 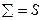 , т.е. совпадает, с (39) – предыдущим определением энтропии. Выражение же (41) – статистическое определение энтропии.
, т.е. совпадает, с (39) – предыдущим определением энтропии. Выражение же (41) – статистическое определение энтропии.
Вычислим теперь статистический интеграл для идеального газа:
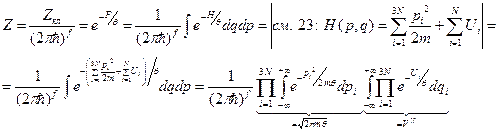
Т.о., 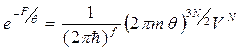
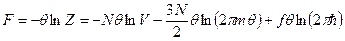
Найдём давление 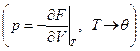 :
: 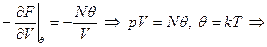
Если возьмём pV=NkT, 1 грамм/моль: pV = RT, N=N* (число Авогадро), тогда pV=N*kT=RT; откуда R=kN*. Т.е. мы получили уравнение состояния идеального газа, и, кстати, значение постоянной Больцмана. Т.е. F – действительно свободная энергия. Действительно, можно показать, что F удовлетворяет 1-ому уравнению Гиббса – Гельмгольца.
Итак, мы
1) обосновали II-ое начало термодинамики, предположив, что работает распределение Гиббса;
2) показали, что статистическое определение энтропии (41) приводит к тому же результату через функцию распределения 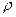 для узкого распределения
для узкого распределения 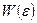 .
.
А что для других функций распределения (в частности для не полностью равновесных систем)?
Здесь введём энтропию, (для произвольной  как (38):
как (38):
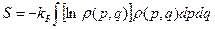 (42)
(42)
Причём эта величина определена на совокупности случайных величин p и q. Если 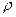 для данного случая – распределение Гиббса, - имеем (38). Вообще говоря, в (42)
для данного случая – распределение Гиббса, - имеем (38). Вообще говоря, в (42) 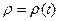 , и следовательно, S = S(t).
, и следовательно, S = S(t).
Что со временем?
Система будет переходить в состояние равновесия, с равновесной функцией распределения. Такая равновесная функция распределения будет, естественно, наиболее вероятной. Можно показать (математически), что при условии постоянства числа частиц в системе (сохранение условий нормировки) и постоянстве внутренней энергии системы в замкнутой системе в ходе процесса эволюции (релаксации) к равновесному состоянию, энтропия, определяемая выражением (42), достигает максимального значения в равновесном состоянии.
Таким образом:
1) 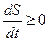
2) максимальная энтропия соответствует наиболее вероятному состоянию;
Частный случай - так называемая теорема Больцмана: так как в идеальном газе при релаксации устанавливается Максвелловское распределение (см. дальше), то при условии постоянства внутренней энергии газа в процессе релаксации энтропия возрастает, а при достижении равновесного состояния остаётся неизменной. Причём процессы возрастания энтропии в большой системе необратимы. Приближенно обратимыми могут быт процессы, при которых 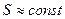 .
.
Проиллюстрируем на примере идеального газа, при его необратимом расширении в пустоту: мгновенно убираем перегородку (см. рисунок)

Вероятность найти весь газ слева при задвинутой перегородке 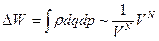 ;
;
Если убрать, то 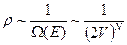 ;
;
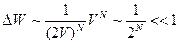 , т.е. газ перейдёт в более вероятное состояние (распределение по всему сосуду, вместо того, чтобы остаться в прежнем объёме).
, т.е. газ перейдёт в более вероятное состояние (распределение по всему сосуду, вместо того, чтобы остаться в прежнем объёме).
С другой стороны 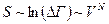 , т.е.
, т.е. 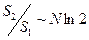 (т.е. тоже очень большая величина, т.е. энтропия вырождена), а
(т.е. тоже очень большая величина, т.е. энтропия вырождена), а 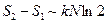 .
.
Дата добавления: 2021-05-28; просмотров: 611;











