Равновесный статистический ансамбль. Роль энергии.

Для системы, находящейся в состоянии статистического (термодинамического) равновесия плотность вероятности ρ явно от времени зависеть не должна:

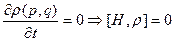(11)

Из механики известно, что любая величина, удовлетворяющая уравнению (11), является интегралом движения уравнений Гамильтона (1), или функцией интегралов движения уравнений (1).

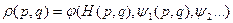, (12) где

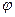- некая функция,

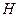- гамильтониан (Н=Е),

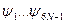- остальные интегралы движения системы (всего 6N интегралов)

Найти их все невозможно, но есть некоторые выделенные.

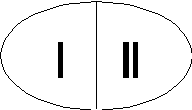
Рассмотрим свойства ρ(q,p) для системы, состоящей из двух независимых подсистем. Тогда очевидно (из теории вероятности):

W=W₁W₂ (dW=dW₁dW₂)

или в силу (4)

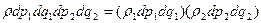
Здесь 1 – для первой подсистемы, а 2 – для второй подсистемы

или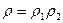

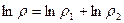(13)

То есть 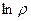- аддитивный интеграл движения, и 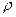должно быть линейной комбинацией аддитивных интегралов движения. В механике всего семь аддитивных интегралов движения: Е (энергия), компоненты импульса 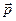и компоненты момента импульса :

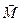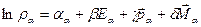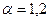, (14)

Причём коэффициенты 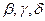должны быть одинаковы для всех подсистем! Если система как целое не движется поступательно или вращательно, то два последних члена можно не учитывать, и

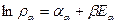(15)

И 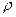зависит только от энергии!!!

(Вспомним из термодинамики – все внутренние параметры являются функциями внешних и энергии для равновесных систем, и если внешние параметры постоянны, то только от энергии!!!)

Вспомним (7):

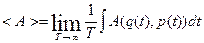- должен зависеть только от Е.

Система, обладающая такими свойствами, называется эргодической, и для неё 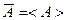в силу (6); а это равенство (8) – эргодическая гипотеза, которая опять должна быть доказана.

Задача: доказать (8) для изолированной системы (каноническое распределение).

Статистическое распределение изолированной системы –