Фазовое пространство.

Основы классической статистики.

Итак, мы начали курс «ТД и СФ» с изучения основных положений (принципов и начал) а также основ математического аппарата термодинамики. При этом мы практически не пользовались представлением о внутренней структуре рассматриваемых систем (равновесных).

Феномен: термодинамике это не нужно. Мы могли бы и дальше двигаться в этом направлении, а пройдя ТД перейти к СФ. Но при этом многие вещи нам пришлось бы делать заново, на что нет времени. Поэтому мы вскоре перейдем к изучению СФ и будем двигаться вперед равномерно как в том так и в другом разделах, опираясь на уже пройденные, знакомые нам вещи.

В основе ТД, как уже указывалось, лежат постулаты, основанные, как правило, на эксперименте (опыте), а также дополнительных эмпирических фактов – напр, уравнение состояния. Физическое (теоретическое) обоснование этих фактов и дает нам СФ, где в основу кладется та или иная модель тела или системы, и на их основе уже получаются основные свойства, в частности, уравнение состояния. СФ не только не изменила основных формулировок принципов ТД, но и продвинулась в понимании. Существенно именно то, что уравнения эти для ТД величин относятся также к средним величинам. О смысле этого понятия поговорим чуть позже, а пока сформулируем основные понятия СФ.

Фазовое пространство.

Рассмотрим макроскопическую систему, состоящую из многих частиц (материальных точек), описываемых классической механикой, и пусть количество этих частиц N. Нас интересует описание их движения. Движение и положение этих частиц задается трехмерным вектором координат (x, y, z) и тремя компонентами скоростей (Vx, Vy, Vz).

Частица имеет три степени свободы (f=3). Если бы мы рассматривали не материальную точку, а, например, двухатомную молекулу, то дела обстояли бы по-другому, и степеней свободы у нее вообще говоря было бы больше.

Далее для простоты удобнее пользоваться обобщенными координатами (в классической механике) и, соответственно, обобщенными импульсами. В данном случае это просто импульсы и координаты. Таким образом, одна частица у нас описывается 6-ю обобщенными координатами, а N частиц – 6N об. координатами.

(3N обобщенных координат и столько же об. импульсов).

Общее число степеней свободы 3N. Если мы знаем все эти 6N величин, мы знаем микросостояние частицы, описываемое точкой в 6-мерном фазовом пространстве, координатами которого являются вышеупомянутые 3 об. координаты и 3 об. импульса.

Иначе – Г (гамма) пространство. Предполагая, что система консервативна, что вполне естественно для таких систем, будем записывать уравнения движения частиц в гамильтоновой форме.

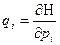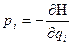; ; (1)

H=(q_1,…,q_f, p_1,…,p_f) – гамильтониан.

С течением времени при изменении микросостояния системы изображающая точка в фазовом пространстве (фазовая точка) будет перемещаться, образуя фазовую траекторию, которая изображает, очевидно, движение всех N частиц. Для классического механического движения решение Ур. Гамильтона однозначно, поэтому фазовые траектории не пересекаются.

Точное решение задачи о поведении системы или ее микроскопической части возможно только путем решения уравнения движения для всех частиц при заданных начальных условиях. Поведение системы – очень сложное. Но возможен вероятностный (статистический) подход, основанный на том, что за достаточно большой промежуток времени система или ее рассматриваемая часть достаточно много раз побывает во всех возможных состояниях.

Обозначим через ∆q∆p некоторый малый участок фазового пространства ∆Г около состояния p,q. ∆Г=∆p1∆p2…∆pfN∆q1…∆qfN.

Можно утверждать, что в течение достаточно долгого времени Т система только некоторую часть времени ∆t находится в этом ∆q∆p.

Величину w= 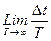(2) можно рассматривать как вероятность найти систему в нашем малом фазовом объеме. Для бесконечно малого участка объема dqdp эта вероятность может быть представлена в виде dw=ρ(q,p)dqdp (4) . Здесь dq и dp есть совокупность по всем qi и pi.

Здесь ρ(q,p) плотность вероятности dw (или ф-я статистического распределения) найти систему в малом промежутке между q,p и dq,dp.

Очевидно, имеет место условие нормировки:

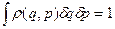(5)

Нахождение статистического распределения заданной системы (или ее подсистемы, вообще говоря незамкнутой) – и есть основная задача стат. физики. Если вычислили ρ(q,p), то можно вычислить вероятность любых значений физических величин, зависящих от состояния системы (p,q). Можем также вычислить среднее значение любой физической величины А.

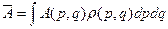(6)

как бы по всем возможным состояниям. Эта величина уже не зависит от микросостояния системы и является макроскопической. Напр, давление, объем, энергия, поляризация и тд.

При достаточно долгих наблюдениях статистический (вероятностный) характер физ. величин не наблюдается, эти величины практически постоянны и равны своим средним значениям и очень редко испытывают заметные отклонения - флуктуации. Речь идет, естественно, о макроскопических величинах, характеризующих систему в целом или же о макроскопической ее части.

В отличие от механического подхода вероятностный подход требует гораздо меньшее количество заданных начальных условий (напр, координат и\или импульсов).

Вопрос: на практике макровеличины определяются обычно как средние по времени.

<A>= 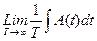(7)

Естественно предположить <A>= 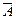(8)

и, вроде, не надо следить за А во времени. Однако, здесь не все так просто, вернемся к этому чуть позже.

зам: если все А= 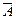, то это статистическое равновесие, ТД равновесие.