Связь между каноническим и микроканоническим распределением.

Есть функция распределения 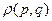- в фазовом пространстве. Можно ввести функцию распределения по энергии W(ε). Когда выводили формулу (18), уже представляли условие нормировки в виде интеграла по энергии (когда вводили 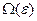- статистический вес)

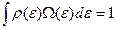
При этом естественно определить W(ε) как

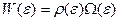(30)

и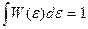

Для изолированной системы (микроканоническое распределение) из (18) имеем:

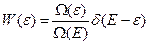(18’)

В случае канонического распределения W(ε) имеет вид

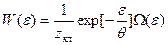(26’)

В (26’) – два сомножителя: 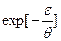(→0 пр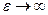и ) и 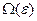- растёт с ε. Например, для идеального газа 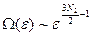(см.(19)). (N>>1)

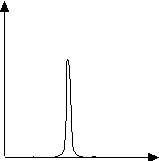
В результате имеем острую функцию с .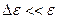

Если подобрать модуль канонического распределения так, что 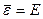, то микроканоническое и каноническое распределения близки, и в принципе (если не интересоваться флуктуациями) можно принять для вычисления среднего в замкнутой системе.

Интересна связь между z_кл и 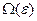. Действительно (см. (27) H=E):

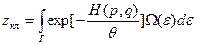(27’) – преобразование Лапласа. Можно написать и обратное. Такая связь подтверждается, если рассмотреть разбиение замкнутой системы на две подсистемы. Тогда, например:

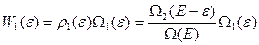см. (22)

Из нормировки 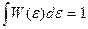следует

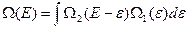(31)

(31) – свёртка!!! Тогда как статистические интегралы перемножаются (см. формулу после (27) 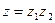) – как и должно быть в преобразовании Лапласа.