Теорема о равномерном распределении кинетической энергии по степеням свободы. Теорема о вириале.
Первую из этих теорем можно доказать с помощью распределения Максвелла, но мы покажем это с помощью более общих соотношений классической механики.
Первая теорема гласит, что на каждую степень свободы приходится кинетическая энергия, равная 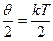 .
.
Доказательство:
Пусть система находится в термостате и справедливо распределение Гиббса: 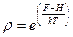 , есть
, есть 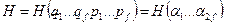 .
.
Рассмотрим среднюю по ансамблю величину:
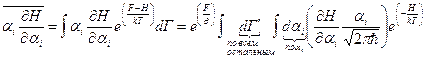 ,
,
где 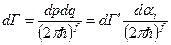 , .т.е.
, .т.е. 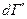 - просто без i-ой переменной.
- просто без i-ой переменной.
Далее:
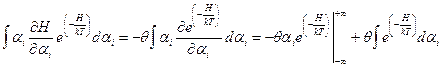
Первая подстановка = 0, и
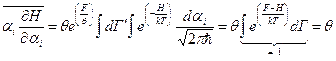 .
.
Таким образом 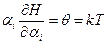 (43)
(43)
Теперь рассмотрим форму для Гамильтониана
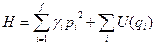 (44)
(44)
(кинетическая энергия + потенциальная энергия). (Как бы считаем, что на каждую степень свободы приходится ki, теперь убеждаемся в этом).
Причём 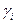 от
от 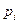 не зависит, может зависеть только от
не зависит, может зависеть только от 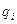 . Например, в декартовой системе координат
. Например, в декартовой системе координат 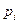 - просто импульс:
- просто импульс: 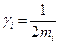 ).
).
Возьмём 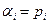 , тогда из (44)
, тогда из (44)
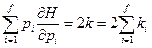
таким образом
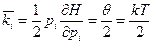 (45)
(45)
Средняя кинетическая энергия всех степеней свободы одинакова и равна 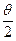 .
.
Если 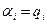 - получим теорему о вириале:
- получим теорему о вириале:
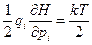 (46)
(46)
Примеры:
1) одноатомный идеальный газ:
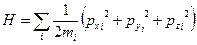
f = 3N; 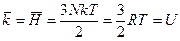 (47)
(47)
2) 2-x атомный идеальный газ
(5 степеней свободы)
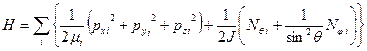 , где
, где 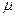 - приведённая масса, J – момент инерции при вращении, а
- приведённая масса, J – момент инерции при вращении, а 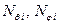 - соответствующие моменты импульса (обобщённые импульсы).
- соответствующие моменты импульса (обобщённые импульсы).
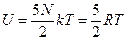 (48)
(48)
3) одномерный осциллятор
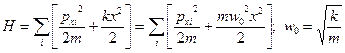
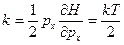 (49)
(49)
Средний вириал:
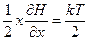 , равенство средней и молекулярной энергии.
, равенство средней и молекулярной энергии.
Таким образом: 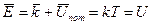
Дата добавления: 2021-05-28; просмотров: 720;











